Learning Physics-Consistent Material Behavior Without Prior Knowledge

Accurately modeling the mechanical behavior of materials is crucial for numerous engineering applications. The quality of these models depends directly on the accuracy of the constitutive law that defines the stress-strain relation. Discovering these constitutive material laws remains a significant challenge, in particular when only material deformation data is available. To address this challenge, unsupervised machine learning methods have been proposed. However, existing approaches have several limitations: they either fail to ensure that the learned constitutive relations are consistent with physical principles, or they rely on a predefined library of constitutive relations or manually crafted input features. These dependencies require significant expertise and specialized domain knowledge. Here, we introduce a machine learning approach called uLED, which overcomes the limitations by using the input convex neural network (ICNN) as the surrogate constitutive model. We improve the optimization strategy for training ICNN, allowing it to be trained end-to-end using direct strain invariants as input across various materials. Furthermore, we utilize the nodal force equilibrium at the internal domain as the training objective, which enables us to learn the constitutive relation solely from temporal displacement recordings. We validate the effectiveness of the proposed method on a diverse range of material laws. We demonstrate that it is robust to a significant level of noise and that it converges to the ground truth with increasing data resolution. We also show that the model can be effectively trained using a displacement field from a subdomain of the test specimen and that the learned constitutive relation from one material sample is transferable to other samples with different geometries. The developed methodology provides an effective tool for discovering constitutive relations.

Sym-Q: Adaptive Symbolic Regression via Sequential Decision-Making

Symbolic regression holds great potential for uncovering underlying mathematical and physical relationships from empirical data. While existing transformer-based models have recently achieved significant success in this domain, they face challenges in terms of generalizability and adaptability. Typically, in cases where the output expressions do not adequately fit experimental data, the models lack efficient mechanisms to adapt or modify the expression. This inflexibility hinders their application in real-world scenarios, particularly in discovering unknown physical or biological relationships. Inspired by how human experts refine and adapt expressions, we introduce Symbolic Q-network (Sym-Q), a novel reinforcement learning-based model that redefines symbolic regression as a sequential decision-making task. Sym-Q leverages supervised demonstrations and refines expressions based on reward signals indicating the quality of fitting precision. Its distinctive ability to manage the complexity of expression trees and perform precise step-wise updates significantly enhances flexibility and efficiency. Our results demonstrate that Sym-Q excels not only in recovering underlying mathematical structures but also uniquely learns to efficiently refine the output expression based on reward signals, thereby discovering underlying expressions. Sym-Q paves the way for more intuitive and impactful discoveries in physical science, marking a substantial advancement in the field of symbolic regression.

Collective Relational Inference for learning physics-consistent heterogeneous particle interactions

Interacting particle systems are ubiquitous in nature and engineering. Revealing particle interaction laws is of fundamental importance but also particularly challenging due to underlying configurational complexities. Recently developed machine learning methods show great potential in discovering pairwise interactions from particle trajectories in homogeneous systems. However, they fail to reveal interactions in heterogeneous systems that are prevalent in reality, where multiple interaction types coexist simultaneously and relational inference is required. Here, we propose a novel probabilistic method for relational inference, which possesses two distinctive characteristics compared to existing methods. First, it infers the interaction types of different edges collectively, and second, it uses a physics-induced graph neural network to learn physics-consistent pairwise interactions. We evaluate the proposed methodology across several benchmark datasets and demonstrate that it is consistent with the underlying physics. Furthermore, we showcase its ability to outperform existing methods in accurately inferring interaction types. In addition, the proposed model is data-efficient and generalizable to large systems when trained on smaller ones, which contrasts with previously proposed solutions. The developed methodology constitutes a key element for the discovery of the fundamental laws that determine macroscopic mechanical properties of particle systems.

Learning Physics-Consistent Particle Interactions

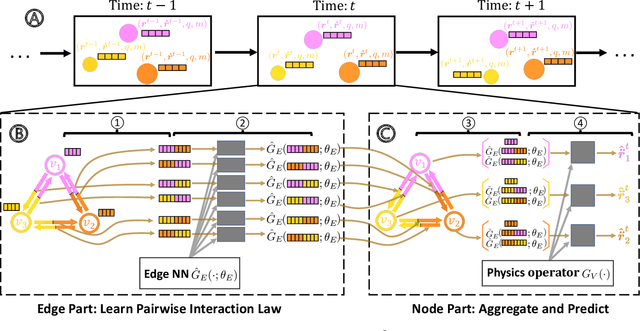
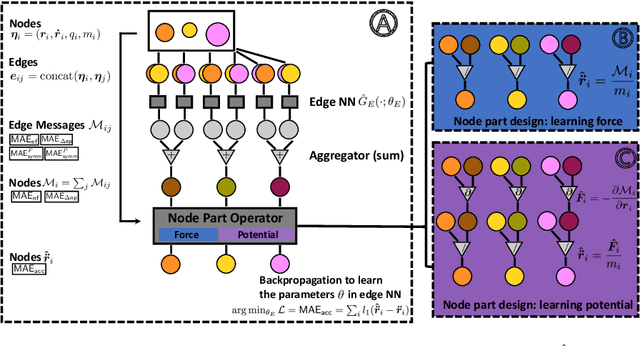
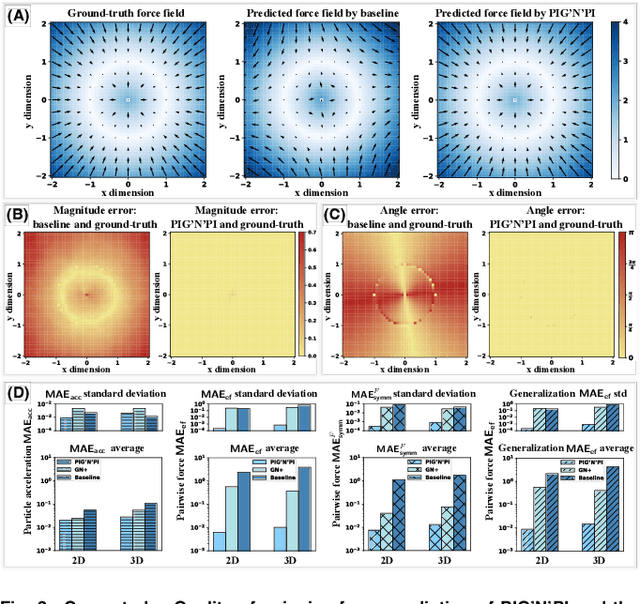
Interacting particle systems play a key role in science and engineering. Access to the governing particle interaction law is fundamental for a complete understanding of such systems. However, the inherent system complexity keeps the particle interaction hidden in many cases. Machine learning methods have the potential to learn the behavior of interacting particle systems by combining experiments with data analysis methods. However, most existing algorithms focus on learning the kinetics at the particle level. Learning pairwise interaction, e.g., pairwise force or pairwise potential energy, remains an open challenge. Here, we propose an algorithm that adapts the Graph Networks framework, which contains an edge part to learn the pairwise interaction and a node part to model the dynamics at particle level. Different from existing approaches that use neural networks in both parts, we design a deterministic operator in the node part. The designed physics operator on the nodes restricts the output space of the edge neural network to be exactly the pairwise interaction. We test the proposed methodology on multiple datasets and demonstrate that it achieves considerably better performance in inferring correctly the pairwise interactions while also being consistent with the underlying physics on all the datasets than existing purely data-driven models. The developed methodology can support a better understanding and discovery of the underlying particle interaction laws, and hence guide the design of materials with targeted properties.