Differential Privacy Guarantees for Stochastic Gradient Langevin Dynamics

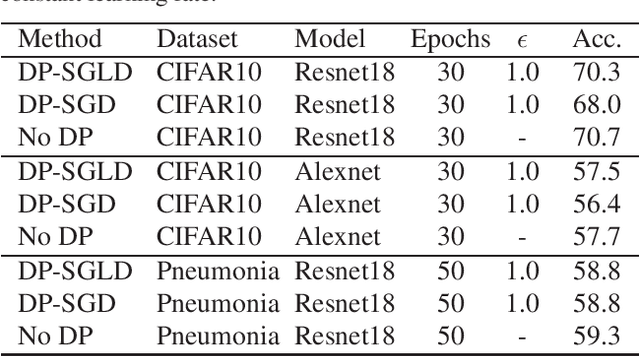
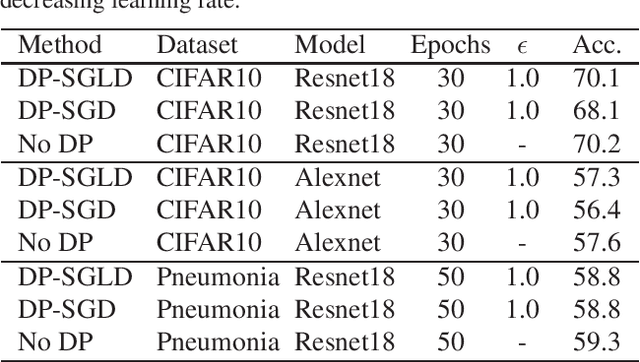
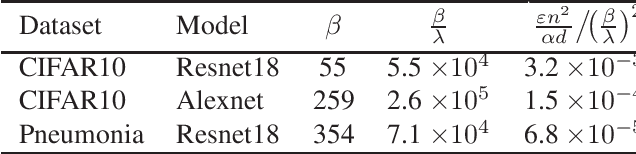
We analyse the privacy leakage of noisy stochastic gradient descent by modeling R\'enyi divergence dynamics with Langevin diffusions. Inspired by recent work on non-stochastic algorithms, we derive similar desirable properties in the stochastic setting. In particular, we prove that the privacy loss converges exponentially fast for smooth and strongly convex objectives under constant step size, which is a significant improvement over previous DP-SGD analyses. We also extend our analysis to arbitrary sequences of varying step sizes and derive new utility bounds. Last, we propose an implementation and our experiments show the practical utility of our approach compared to classical DP-SGD libraries.

ARIANN: Low-Interaction Privacy-Preserving Deep Learning via Function Secret Sharing

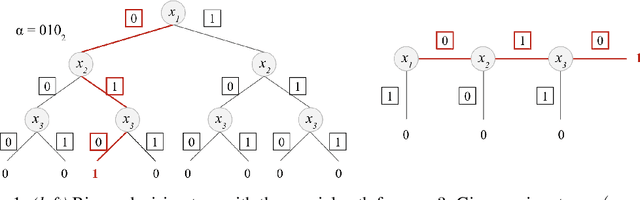
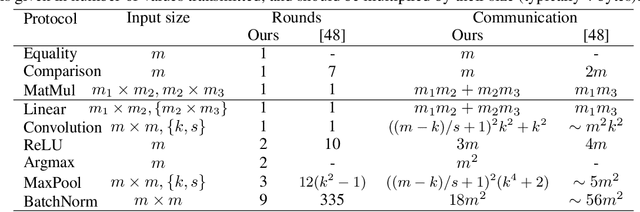
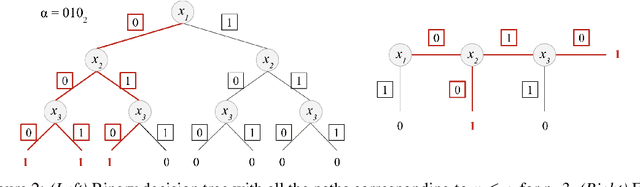
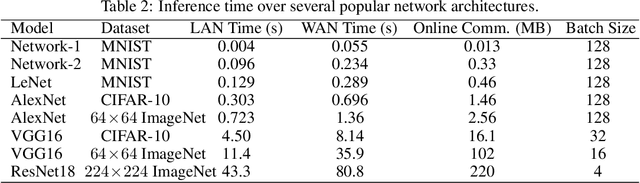
We propose ARIANN, a low-interaction framework to perform private training and inference of standard deep neural networks on sensitive data. This framework implements semi-honest 2-party computation and leverages function secret sharing, a recent cryptographic protocol that only uses lightweight primitives to achieve an efficient online phase with a single message of the size of the inputs, for operations like comparison and multiplication which are building blocks of neural networks. Built on top of PyTorch, it offers a wide range of functions including ReLU, MaxPool and BatchNorm, and allows to use models like AlexNet or ResNet18. We report experimental results for inference and training over distant servers. Last, we propose an extension to support n-party private federated learning.

Partially Encrypted Machine Learning using Functional Encryption

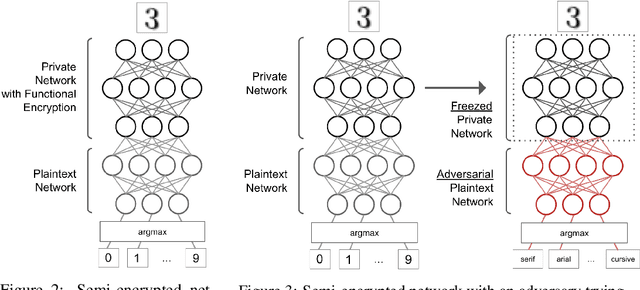
Machine learning on encrypted data has received a lot of attention thanks to recent breakthroughs in homomorphic encryption and secure multi-party computation. It allows outsourcing computation to untrusted servers without sacrificing privacy of sensitive data. We propose a practical framework to perform partially encrypted and privacy-preserving predictions which combines adversarial training and functional encryption. We first present a new functional encryption scheme to efficiently compute quadratic functions so that the data owner controls what can be computed but is not involved in the calculation: it provides a decryption key which allows one to learn a specific function evaluation of some encrypted data. We then show how to use it in machine learning to partially encrypt neural networks with quadratic activation functions at evaluation time, and we provide a thorough analysis of the information leaks based on indistinguishability of data items of the same label. Last, since most encryption schemes cannot deal with the last thresholding operation used for classification, we propose a training method to prevent selected sensitive features from leaking, which adversarially optimizes the network against an adversary trying to identify these features. This is interesting for several existing works using partially encrypted machine learning as it comes with little reduction on the model's accuracy and significantly improves data privacy.