CoMadOut -- A Robust Outlier Detection Algorithm based on CoMAD

Unsupervised learning methods are well established in the area of anomaly detection and achieve state of the art performances on outlier data sets. Outliers play a significant role, since they bear the potential to distort the predictions of a machine learning algorithm on a given data set. Especially among PCA-based methods, outliers have an additional destructive potential regarding the result: they may not only distort the orientation and translation of the principal components, they also make it more complicated to detect outliers. To address this problem, we propose the robust outlier detection algorithm CoMadOut, which satisfies two required properties: (1) being robust towards outliers and (2) detecting them. Our outlier detection method using coMAD-PCA defines dependent on its variant an inlier region with a robust noise margin by measures of in-distribution (ID) and out-of-distribution (OOD). These measures allow distribution based outlier scoring for each principal component, and thus, for an appropriate alignment of the decision boundary between normal and abnormal instances. Experiments comparing CoMadOut with traditional, deep and other comparable robust outlier detection methods showed that the performance of the introduced CoMadOut approach is competitive to well established methods related to average precision (AP), recall and area under the receiver operating characteristic (AUROC) curve. In summary our approach can be seen as a robust alternative for outlier detection tasks.

Enhancing cluster analysis via topological manifold learning

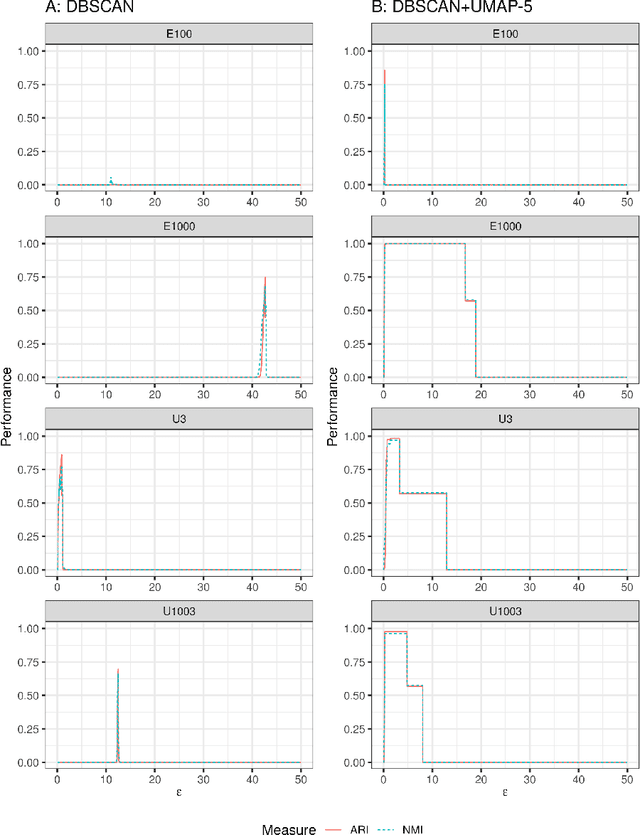
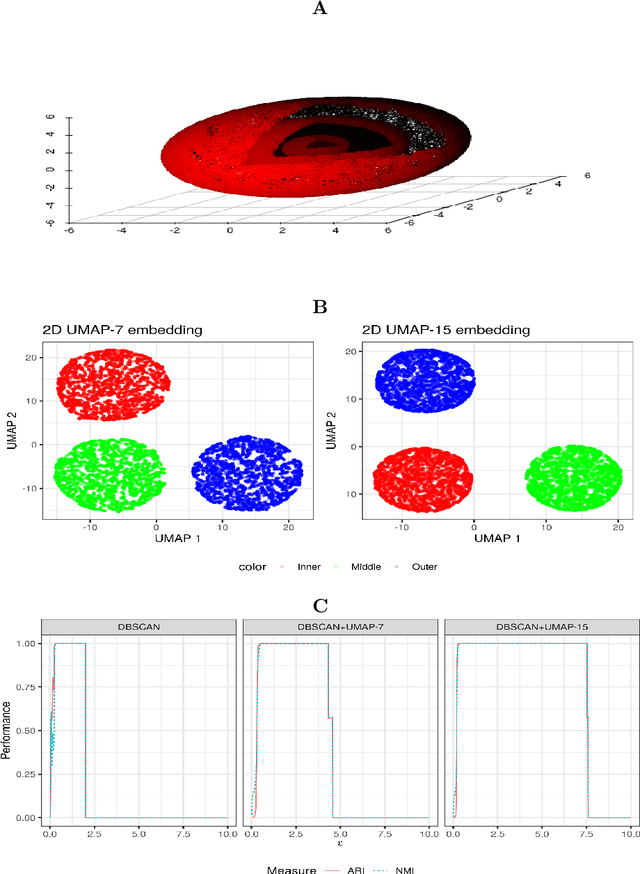
We discuss topological aspects of cluster analysis and show that inferring the topological structure of a dataset before clustering it can considerably enhance cluster detection: theoretical arguments and empirical evidence show that clustering embedding vectors, representing the structure of a data manifold instead of the observed feature vectors themselves, is highly beneficial. To demonstrate, we combine manifold learning method UMAP for inferring the topological structure with density-based clustering method DBSCAN. Synthetic and real data results show that this both simplifies and improves clustering in a diverse set of low- and high-dimensional problems including clusters of varying density and/or entangled shapes. Our approach simplifies clustering because topological pre-processing consistently reduces parameter sensitivity of DBSCAN. Clustering the resulting embeddings with DBSCAN can then even outperform complex methods such as SPECTACL and ClusterGAN. Finally, our investigation suggests that the crucial issue in clustering does not appear to be the nominal dimension of the data or how many irrelevant features it contains, but rather how \textit{separable} the clusters are in the ambient observation space they are embedded in, which is usually the (high-dimensional) Euclidean space defined by the features of the data. Our approach is successful because we perform the cluster analysis after projecting the data into a more suitable space that is optimized for separability, in some sense.