Probably approximately correct learning of Horn envelopes from queries

We propose an algorithm for learning the Horn envelope of an arbitrary domain using an expert, or an oracle, capable of answering certain types of queries about this domain. Attribute exploration from formal concept analysis is a procedure that solves this problem, but the number of queries it may ask is exponential in the size of the resulting Horn formula in the worst case. We recall a well-known polynomial-time algorithm for learning Horn formulas with membership and equivalence queries and modify it to obtain a polynomial-time probably approximately correct algorithm for learning the Horn envelope of an arbitrary domain.

On the Usability of Probably Approximately Correct Implication Bases

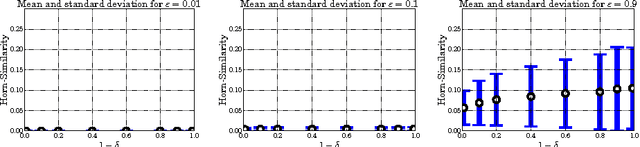
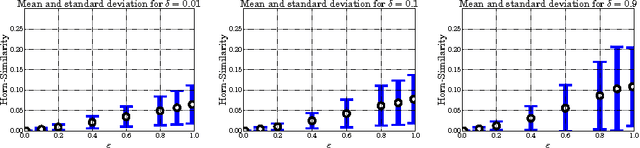
We revisit the notion of probably approximately correct implication bases from the literature and present a first formulation in the language of formal concept analysis, with the goal to investigate whether such bases represent a suitable substitute for exact implication bases in practical use-cases. To this end, we quantitatively examine the behavior of probably approximately correct implication bases on artificial and real-world data sets and compare their precision and recall with respect to their corresponding exact implication bases. Using a small example, we also provide qualitative insight that implications from probably approximately correct bases can still represent meaningful knowledge from a given data set.

Abstract Attribute Exploration with Partial Object Descriptions

Attribute exploration has been investigated in several studies, with particular emphasis on the algorithmic aspects of this knowledge acquisition method. In its basic version the method itself is rather simple and transparent. But when background knowledge and partially described counter-examples are admitted, it gets more difficult. Here we discuss this case in an abstract, somewhat "axiomatic" setting, providing a terminology that clarifies the abstract strategy of the method rather than its algorithmic implementation.