Closed-Loop phase selection in EEG-TMS using Bayesian Optimization

Research on transcranial magnetic stimulation (TMS) combined with encephalography feedback (EEG-TMS) has shown that the phase of the sensorimotor mu rhythm is predictive of corticospinal excitability. Thus, if the subject-specific optimal phase is known, stimulation can be timed to be more efficient. In this paper, we present a closed-loop algorithm to determine the optimal phase linked to the highest excitability with few trials. We used Bayesian optimization as an automated, online search tool in an EEG-TMS simulation experiment. From a sample of 38 participants, we selected all participants with a significant single-subject phase effect (N = 5) for simulation. We then simulated 1000 experimental sessions per participant where we used Bayesian optimization to find the optimal phase. We tested two objective functions: Fitting a sinusoid in Bayesian linear regression or Gaussian Process (GP) regression. We additionally tested adaptive sampling using a knowledge gradient as the acquisition function compared with random sampling. We evaluated the algorithm's performance in a fast optimization (100 trials) and a long-term optimization (1000 trials). For fast optimization, the Bayesian linear regression in combination with adaptive sampling gives the best results with a mean phase location accuracy of 79 % after 100 trials. With either sampling approach, Bayesian linear regression performs better than GP regression in the fast optimization. In the long-term optimization, Bayesian regression with random sampling shows the best trajectory, with a rather steep improvement and good final performance of 87 % mean phase location accuracy. We show the suitability of closed-loop Bayesian optimization for phase selection. We could increase the speed and accuracy by using prior knowledge about the expected function shape compared with traditional Bayesian optimization with GP regression.

Latent Event-Predictive Encodings through Counterfactual Regularization

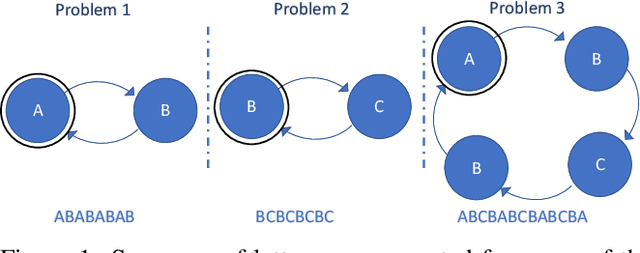
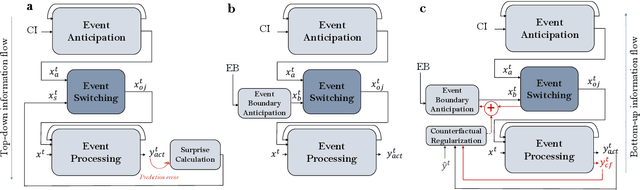
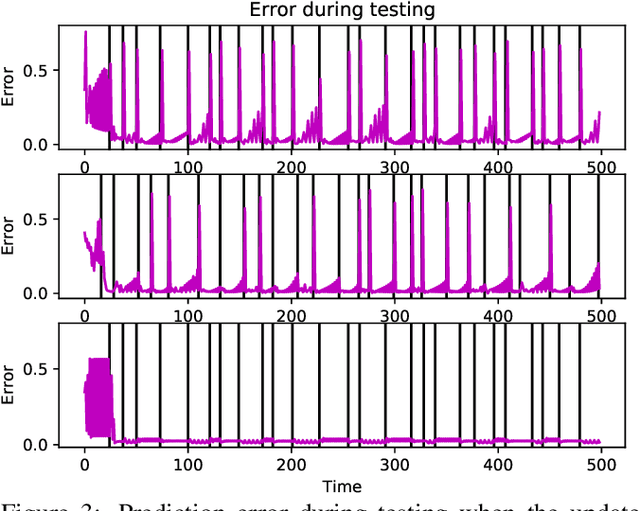
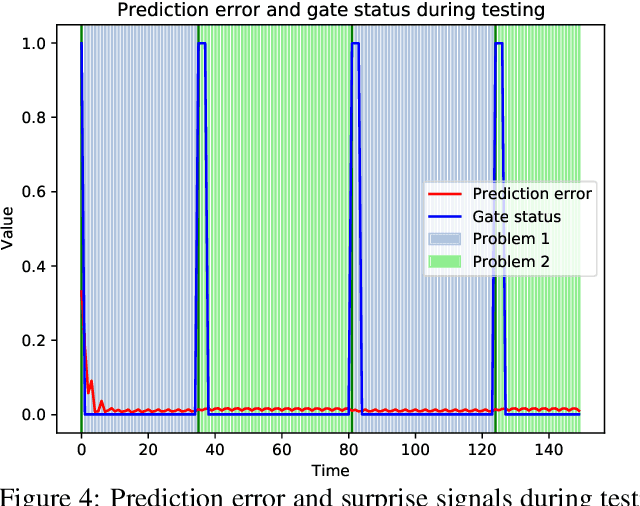
A critical challenge for any intelligent system is to infer structure from continuous data streams. Theories of event-predictive cognition suggest that the brain segments sensorimotor information into compact event encodings, which are used to anticipate and interpret environmental dynamics. Here, we introduce a SUrprise-GAted Recurrent neural network (SUGAR) using a novel form of counterfactual regularization. We test the model on a hierarchical sequence prediction task, where sequences are generated by alternating hidden graph structures. Our model learns to both compress the temporal dynamics of the task into latent event-predictive encodings and anticipate event transitions at the right moments, given noisy hidden signals about them. The addition of the counterfactual regularization term ensures fluid transitions from one latent code to the next, whereby the resulting latent codes exhibit compositional properties. The implemented mechanisms offer a host of useful applications in other domains, including hierarchical reasoning, planning, and decision making.

Fostering Event Compression using Gated Surprise

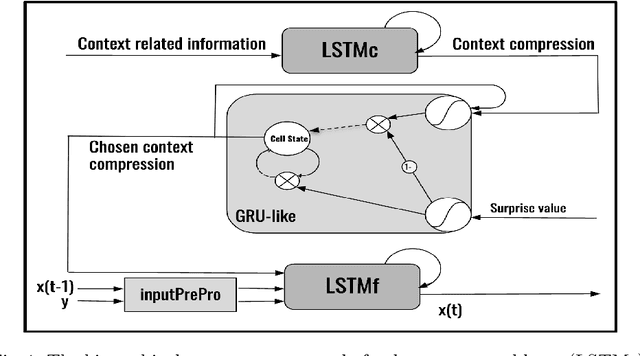
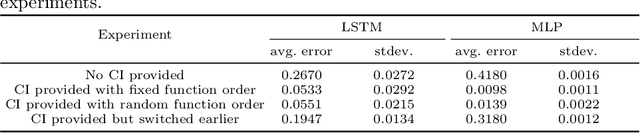
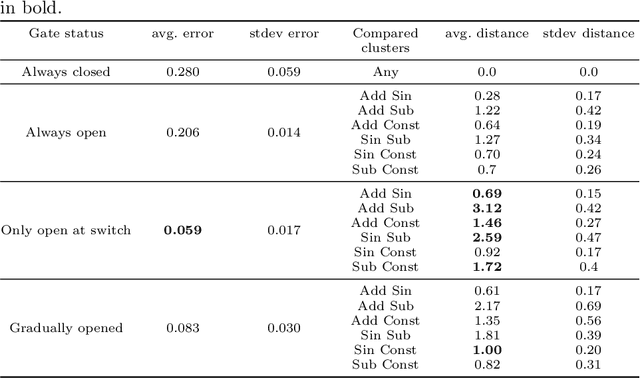
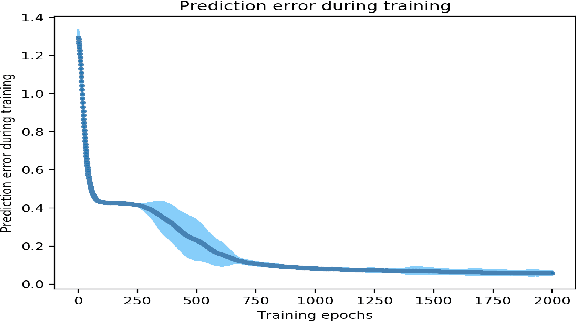
Our brain receives a dynamically changing stream of sensorimotor data. Yet, we perceive a rather organized world, which we segment into and perceive as events. Computational theories of cognitive science on event-predictive cognition suggest that our brain forms generative, event-predictive models by segmenting sensorimotor data into suitable chunks of contextual experiences. Here, we introduce a hierarchical, surprise-gated recurrent neural network architecture, which models this process and develops compact compressions of distinct event-like contexts. The architecture contains a contextual LSTM layer, which develops generative compressions of ongoing and subsequent contexts. These compressions are passed into a GRU-like layer, which uses surprise signals to update its recurrent latent state. The latent state is passed forward into another LSTM layer, which processes actual dynamic sensory flow in the light of the provided latent, contextual compression signals. Our model shows to develop distinct event compressions and achieves the best performance on multiple event processing tasks. The architecture may be very useful for the further development of resource-efficient learning, hierarchical model-based reinforcement learning, as well as the development of artificial event-predictive cognition and intelligence.

Learning, Planning, and Control in a Monolithic Neural Event Inference Architecture

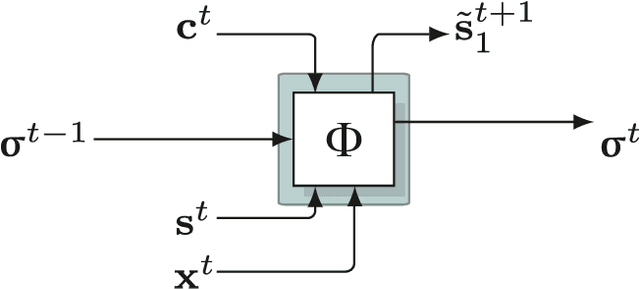
We introduce a dynamic artificial neural network-based (ANN) adaptive inference process, which learns temporal predictive models of dynamical systems. We term the process REPRISE, a REtrospective and PRospective Inference SchEme. REPRISE infers the unobservable contextual state that best explains its recently encountered sensorimotor experiences as well as accompanying, context-dependent temporal predictive models retrospectively. Meanwhile, it executes prospective inference, optimizing upcoming motor activities in a goal-directed manner. In a first implementation, a recurrent neural network (RNN) is trained to learn a temporal forward model, which predicts the sensorimotor contingencies of different simulated dynamic vehicles. The RNN is augmented with contextual neurons, which enable the compact encoding of distinct, but related sensorimotor dynamics. We show that REPRISE is able to concurrently learn to separate and approximate the encountered sensorimotor dynamics. Moreover, we show that REPRISE can exploit the learned model to induce goal-directed, model-predictive control, that is, approximate active inference: Given a goal state, the system imagines a motor command sequence optimizing it with the prospective objective to minimize the distance to a given goal. Meanwhile, the system evaluates the encountered sensorimotor contingencies retrospectively, adapting its neural hidden states for maintaining model coherence. The RNN activities thus continuously imagine the upcoming future and reflect on the recent past, optimizing both, hidden state and motor activities. In conclusion, the combination of temporal predictive structures with modulatory, generative encodings offers a way to develop compact event codes, which selectively activate particular types of sensorimotor event-specific dynamics.