Quantum-enhanced least-square support vector machine: simplified quantum algorithm and sparse solutions

Quantum algorithms can enhance machine learning in different aspects. Here, we study quantum-enhanced least-square support vector machine (LS-SVM). Firstly, a novel quantum algorithm that uses continuous variable to assist matrix inversion is introduced to simplify the algorithm for quantum LS-SVM, while retaining exponential speed-up. Secondly, we propose a hybrid quantum-classical version for sparse solutions of LS-SVM. By encoding a large dataset into a quantum state, a much smaller transformed dataset can be extracted using quantum matrix toolbox, which is further processed in classical SVM. We also incorporate kernel methods into the above quantum algorithms, which uses both exponential growth Hilbert space of qubits and infinite dimensionality of continuous variable for quantum feature maps. The quantum LS-SVM exploits quantum properties to explore important themes for SVM such as sparsity and kernel methods, and stresses its quantum advantages ranging from speed-up to the potential capacity to solve classically difficult machine learning tasks.

Physical implementation of quantum nonparametric learning with trapped ions

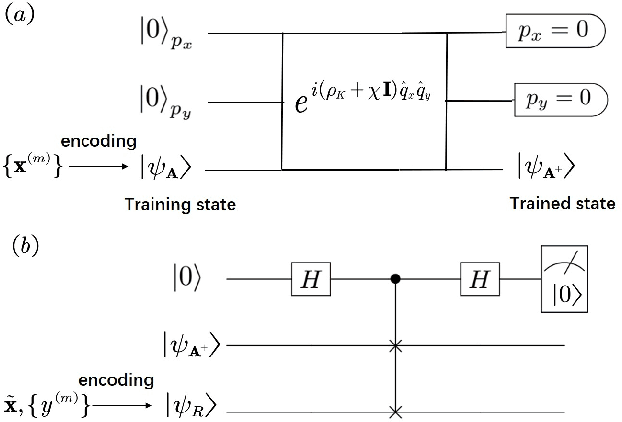
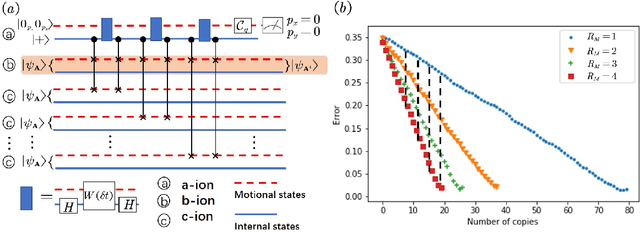
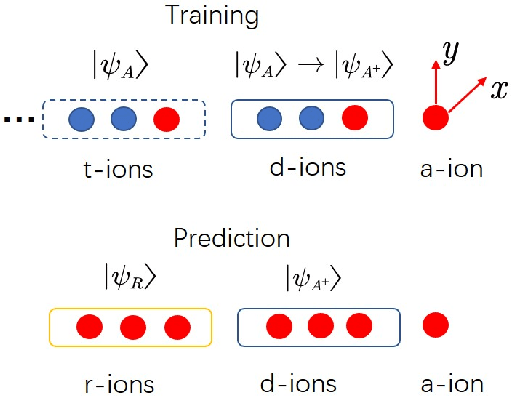
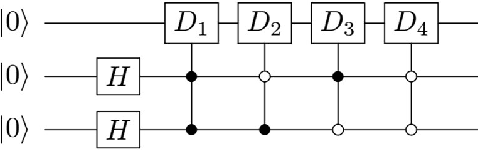
Nonparametric learning is able to make reliable predictions by extracting information from similarities between a new set of input data and all samples. Here we point out a quantum paradigm of nonparametric learning which offers an exponential speedup over the sample size. By encoding data into quantum feature space, similarity between the data is defined as an inner product of quantum states. A quantum training state is introduced to superpose all data of samples, encoding relevant information for learning its bipartite entanglement spectrum. We demonstrate that a trained state for prediction can be obtained by entanglement spectrum transformation, using quantum matrix toolbox. We further workout a feasible scheme to implement the quantum nonparametric learning with trapped ions, and demonstrate the power of quantum superposition for machine leaning with a state-of-the-art technology

Nonlinear regression based on a hybrid quantum computer

Incorporating nonlinearity into quantum machine learning is essential for learning a complicated input-output mapping. We here propose quantum algorithms for nonlinear regression, where nonlinearity is introduced with feature maps when loading classical data into quantum states. Our implementation is based on a hybrid quantum computer, exploiting both discrete and continuous variables, for their capacity to encode novel features and efficiency of processing information. We propose encoding schemes that can realize well-known polynomial and Gaussian kernel ridge regressions, with exponentially speed-up regarding to the number of samples.

Realizing quantum linear regression with auxiliary qumodes

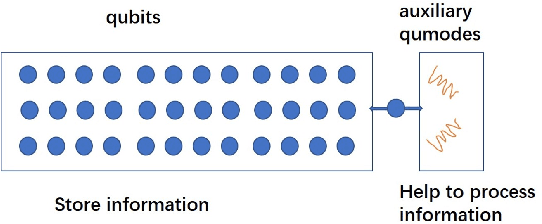
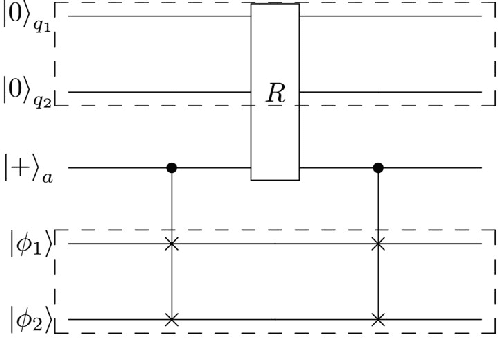
In order to exploit quantum advantages, quantum algorithms are indispensable for operating machine learning with quantum computers. We here propose an intriguing hybrid approach of quantum information processing for quantum linear regression, which utilizes both discrete and continuous quantum variables, in contrast to existing wisdoms based solely upon discrete qubits. In our framework, data information is encoded in a qubit system, while information processing is tackled using auxiliary continuous qumodes via qubit-qumode interactions. Moreover, it is also elaborated that finite squeezing is quite helpful for efficiently running the quantum algorithms in realistic setup. Comparing with an all-qubit approach, the present hybrid approach is more efficient and feasible for implementing quantum algorithms, still retaining exponential quantum speed-up.