A tractable ellipsoidal approximation for voltage regulation problems

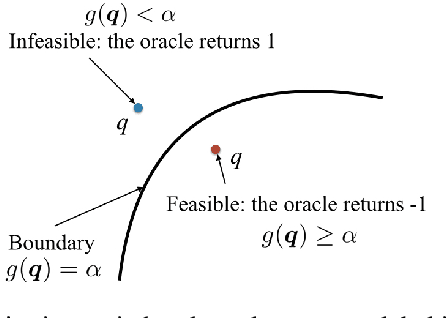
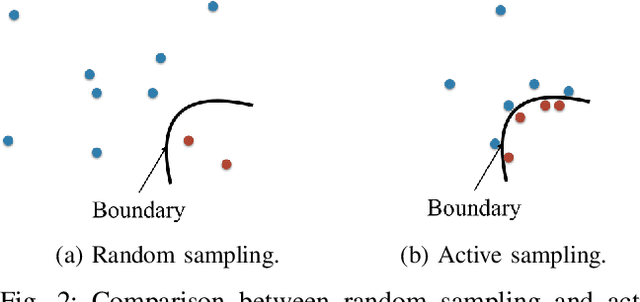
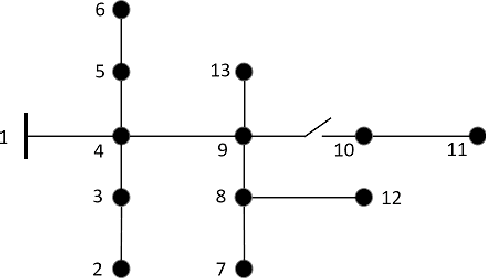
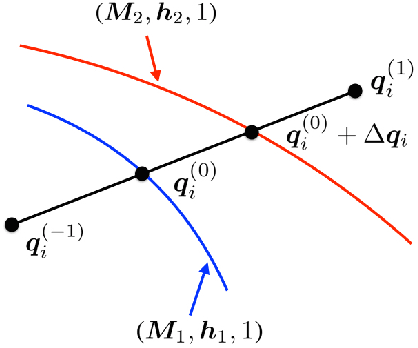
We present a machine learning approach to the solution of chance constrained optimizations in the context of voltage regulation problems in power system operation. The novelty of our approach resides in approximating the feasible region of uncertainty with an ellipsoid. We formulate this problem using a learning model similar to Support Vector Machines (SVM) and propose a sampling algorithm that efficiently trains the model. We demonstrate our approach on a voltage regulation problem using standard IEEE distribution test feeders.

Distribution System Voltage Control under Uncertainties using Tractable Chance Constraints

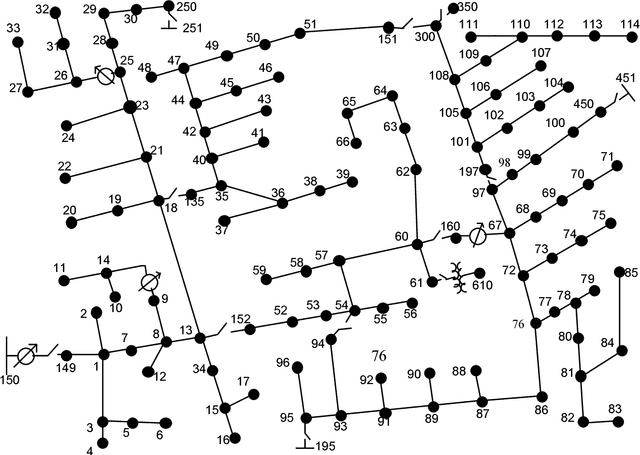
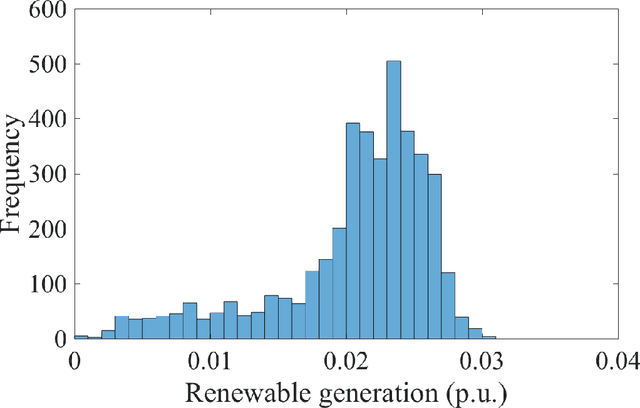
Voltage control plays an important role in the operation of electricity distribution networks, especially with high penetration of distributed energy resources. These resources introduce significant and fast varying uncertainties. In this paper, we focus on reactive power compensation to control voltage in the presence of uncertainties. We adopt a chance constraint approach that accounts for arbitrary correlations between renewable resources at each of the buses. We show how the problem can be solved efficiently using historical samples via a stochastic quasi gradient method. We also show that this optimization problem is convex for a wide variety of probabilistic distributions. Compared to conventional per-bus chance constraints, our formulation is more robust to uncertainty and more computationally tractable. We illustrate the results using standard IEEE distribution test feeders.