Manifold Sampling via Entropy Maximization

Sampling from constrained distributions has a wide range of applications, including in Bayesian optimization and robotics. Prior work establishes convergence and feasibility guarantees for constrained sampling, but assumes that the feasible set is connected. However, in practice, the feasible set often decomposes into multiple disconnected components, which makes efficient sampling under constraints challenging. In this paper, we propose MAnifold Sampling via Entropy Maximization (MASEM) for sampling on a manifold with an unknown number of disconnected components, implicitly defined by smooth equality and inequality constraints. The presented method uses a resampling scheme to maximize the entropy of the empirical distribution based on k-nearest neighbor density estimation. We show that, in the mean field, MASEM decreases the KL-divergence between the empirical distribution and the maximum-entropy target exponentially in the number of resampling steps. We instantiate MASEM with multiple local samplers and demonstrate its versatility and efficiency on synthetic and robotics-based benchmarks. MASEM enables fast and scalable mixing across a range of constrained sampling problems, improving over alternatives by an order of magnitude in Sinkhorn distance with competitive runtime.

Constrained Sampling to Guide Universal Manipulation RL

We consider how model-based solvers can be leveraged to guide training of a universal policy to control from any feasible start state to any feasible goal in a contact-rich manipulation setting. While Reinforcement Learning (RL) has demonstrated its strength in such settings, it may struggle to sufficiently explore and discover complex manipulation strategies, especially in sparse-reward settings. Our approach is based on the idea of a lower-dimensional manifold of feasible, likely-visited states during such manipulation and to guide RL with a sampler from this manifold. We propose Sample-Guided RL, which uses model-based constraint solvers to efficiently sample feasible configurations (satisfying differentiable collision, contact, and force constraints) and leverage them to guide RL for universal (goal-conditioned) manipulation policies. We study using this data directly to bias state visitation, as well as using black-box optimization of open-loop trajectories between random configurations to impose a state bias and optionally add a behavior cloning loss. In a minimalistic double sphere manipulation setting, Sample-Guided RL discovers complex manipulation strategies and achieves high success rates in reaching any statically stable state. In a more challenging panda arm setting, our approach achieves a significant success rate over a near-zero baseline, and demonstrates a breadth of complex whole-body-contact manipulation strategies.

Meta-Optimization and Program Search using Language Models for Task and Motion Planning

Intelligent interaction with the real world requires robotic agents to jointly reason over high-level plans and low-level controls. Task and motion planning (TAMP) addresses this by combining symbolic planning and continuous trajectory generation. Recently, foundation model approaches to TAMP have presented impressive results, including fast planning times and the execution of natural language instructions. Yet, the optimal interface between high-level planning and low-level motion generation remains an open question: prior approaches are limited by either too much abstraction (e.g., chaining simplified skill primitives) or a lack thereof (e.g., direct joint angle prediction). Our method introduces a novel technique employing a form of meta-optimization to address these issues by: (i) using program search over trajectory optimization problems as an interface between a foundation model and robot control, and (ii) leveraging a zero-order method to optimize numerical parameters in the foundation model output. Results on challenging object manipulation and drawing tasks confirm that our proposed method improves over prior TAMP approaches.

Stein Variational Evolution Strategies

Stein Variational Gradient Descent (SVGD) is a highly efficient method to sample from an unnormalized probability distribution. However, the SVGD update relies on gradients of the log-density, which may not always be available. Existing gradient-free versions of SVGD make use of simple Monte Carlo approximations or gradients from surrogate distributions, both with limitations. To improve gradient-free Stein variational inference, we combine SVGD steps with evolution strategy (ES) updates. Our results demonstrate that the resulting algorithm generates high-quality samples from unnormalized target densities without requiring gradient information. Compared to prior gradient-free SVGD methods, we find that the integration of the ES update in SVGD significantly improves the performance on multiple challenging benchmark problems.

NLP Sampling: Combining MCMC and NLP Methods for Diverse Constrained Sampling

Generating diverse samples under hard constraints is a core challenge in many areas. With this work we aim to provide an integrative view and framework to combine methods from the fields of MCMC, constrained optimization, as well as robotics, and gain insights in their strengths from empirical evaluations. We propose NLP Sampling as a general problem formulation, propose a family of restarting two-phase methods as a framework to integrated methods from across the fields, and evaluate them on analytical and robotic manipulation planning problems. Complementary to this, we provide several conceptual discussions, e.g. on the role of Lagrange parameters, global sampling, and the idea of a Diffused NLP and a corresponding model-based denoising sampler.

RHH-LGP: Receding Horizon And Heuristics-Based Logic-Geometric Programming For Task And Motion Planning

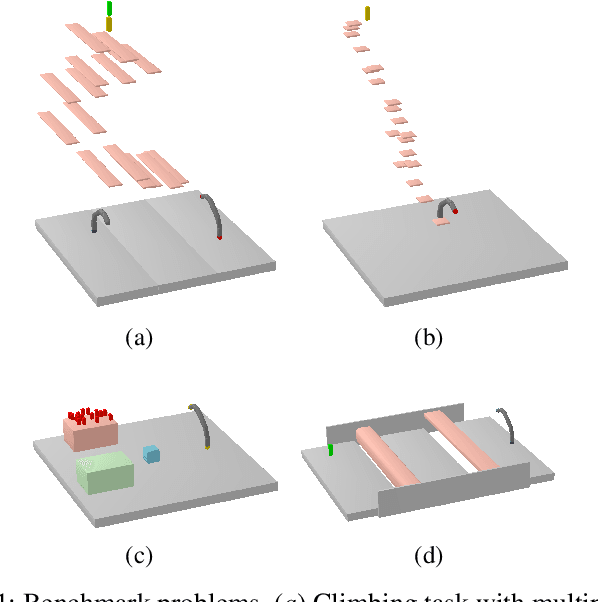
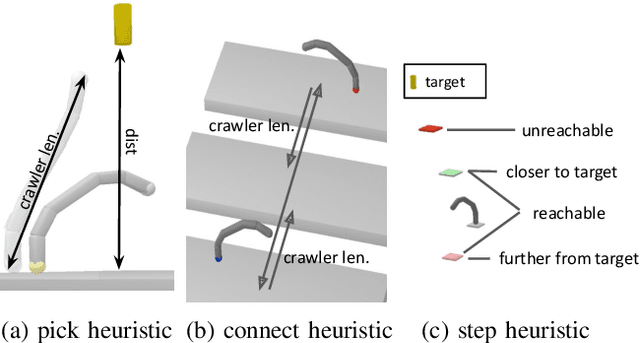
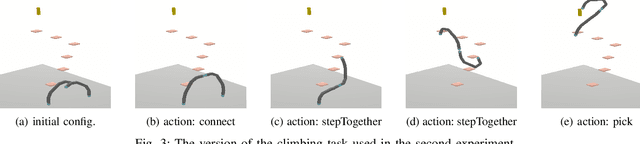
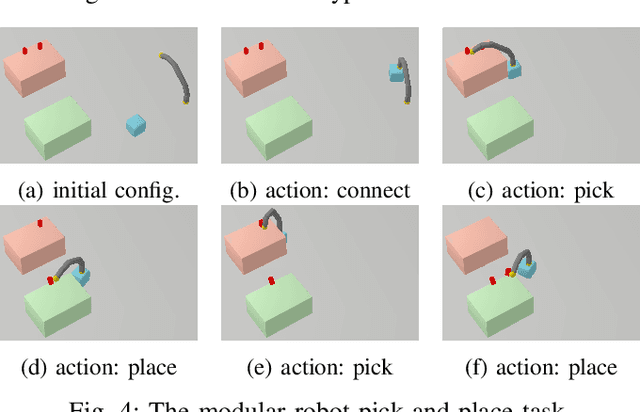
Sequential decision-making and motion planning for robotic manipulation induce combinatorial complexity. For long-horizon tasks, especially when the environment comprises many objects that can be interacted with, planning efficiency becomes even more important. To plan such long-horizon tasks, we present the RHH-LGP algorithm for combined task and motion planning (TAMP). First, we propose a TAMP approach (based on Logic-Geometric Programming) that effectively uses geometry-based heuristics for solving long-horizon manipulation tasks. We further improve the efficiency of this planner by a receding horizon formulation, resulting in RHH-LGP. We demonstrate the effectiveness and generality of our approach on several long-horizon tasks that require reasoning about interactions with a large number of objects. Using our framework, we can solve tasks that require multiple robots, including a mobile robot and snake-like walking robots, to form novel heterogeneous kinematic structures autonomously.