Single-Solution Hypervolume Maximization and its use for Improving Generalization of Neural Networks

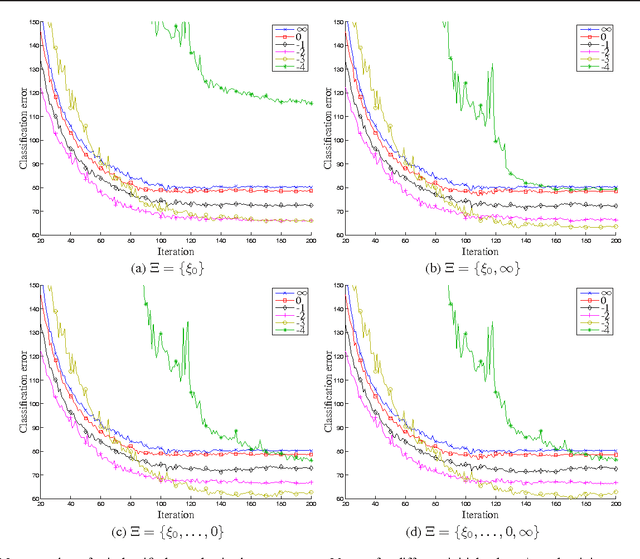
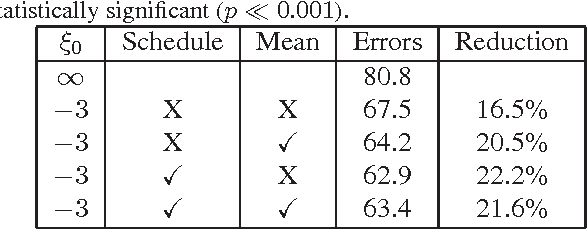
This paper introduces the hypervolume maximization with a single solution as an alternative to the mean loss minimization. The relationship between the two problems is proved through bounds on the cost function when an optimal solution to one of the problems is evaluated on the other, with a hyperparameter to control the similarity between the two problems. This same hyperparameter allows higher weight to be placed on samples with higher loss when computing the hypervolume's gradient, whose normalized version can range from the mean loss to the max loss. An experiment on MNIST with a neural network is used to validate the theory developed, showing that the hypervolume maximization can behave similarly to the mean loss minimization and can also provide better performance, resulting on a 20% reduction of the classification error on the test set.

Reducing the Training Time of Neural Networks by Partitioning

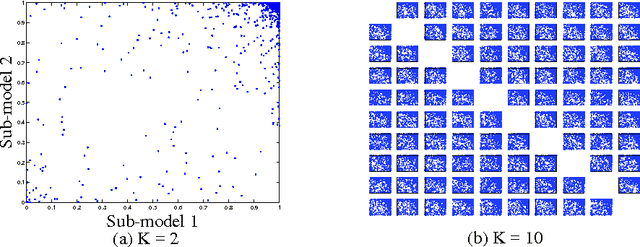
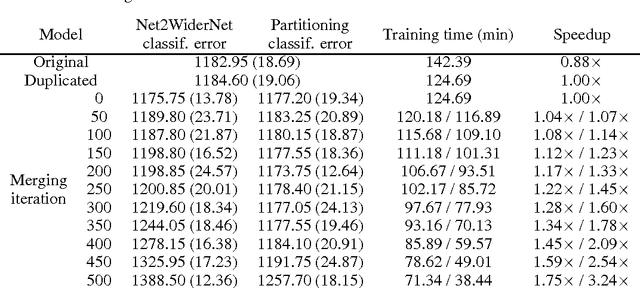
This paper presents a new method for pre-training neural networks that can decrease the total training time for a neural network while maintaining the final performance, which motivates its use on deep neural networks. By partitioning the training task in multiple training subtasks with sub-models, which can be performed independently and in parallel, it is shown that the size of the sub-models reduces almost quadratically with the number of subtasks created, quickly scaling down the sub-models used for the pre-training. The sub-models are then merged to provide a pre-trained initial set of weights for the original model. The proposed method is independent of the other aspects of the training, such as architecture of the neural network, training method, and objective, making it compatible with a wide range of existing approaches. The speedup without loss of performance is validated experimentally on MNIST and on CIFAR10 data sets, also showing that even performing the subtasks sequentially can decrease the training time. Moreover, we show that larger models may present higher speedups and conjecture about the benefits of the method in distributed learning systems.

Asymmetric Distributions from Constrained Mixtures

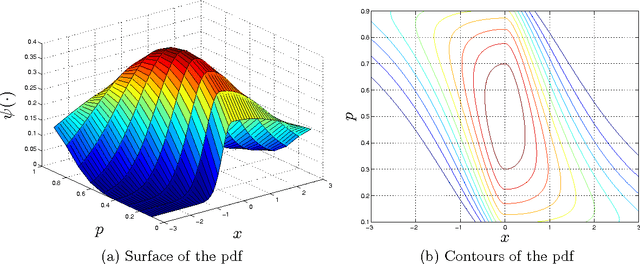
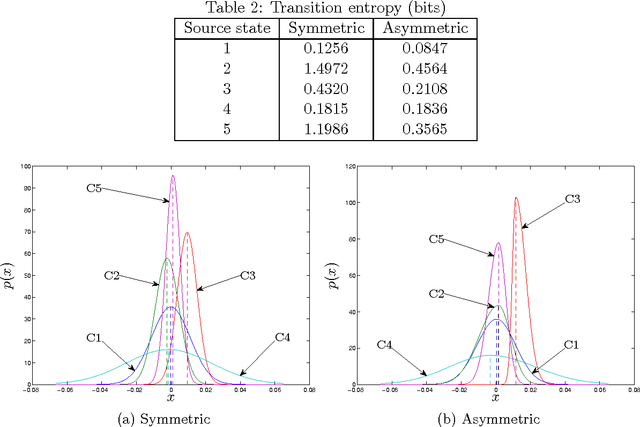
This paper introduces constrained mixtures for continuous distributions, characterized by a mixture of distributions where each distribution has a shape similar to the base distribution and disjoint domains. This new concept is used to create generalized asymmetric versions of the Laplace and normal distributions, which are shown to define exponential families, with known conjugate priors, and to have maximum likelihood estimates for the original parameters, with known closed-form expressions. The asymmetric and symmetric normal distributions are compared in a linear regression example, showing that the asymmetric version performs at least as well as the symmetric one, and in a real world time-series problem, where a hidden Markov model is used to fit a stock index, indicating that the asymmetric version provides higher likelihood and may learn distribution models over states and transition distributions with considerably less entropy.