Single-Solution Hypervolume Maximization and its use for Improving Generalization of Neural Networks

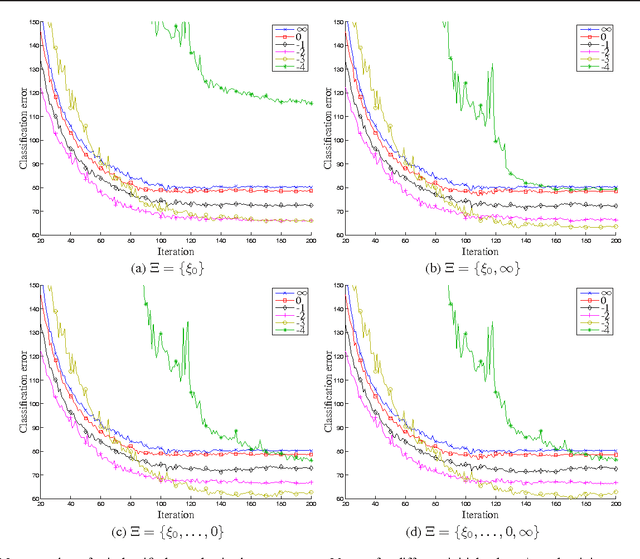
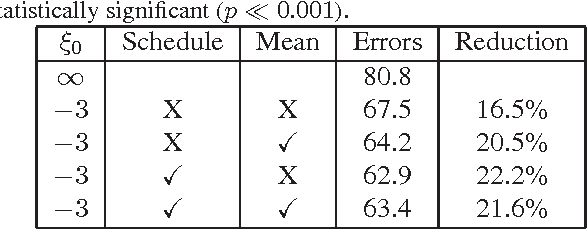
This paper introduces the hypervolume maximization with a single solution as an alternative to the mean loss minimization. The relationship between the two problems is proved through bounds on the cost function when an optimal solution to one of the problems is evaluated on the other, with a hyperparameter to control the similarity between the two problems. This same hyperparameter allows higher weight to be placed on samples with higher loss when computing the hypervolume's gradient, whose normalized version can range from the mean loss to the max loss. An experiment on MNIST with a neural network is used to validate the theory developed, showing that the hypervolume maximization can behave similarly to the mean loss minimization and can also provide better performance, resulting on a 20% reduction of the classification error on the test set.