Asymmetric Distributions from Constrained Mixtures
Paper and Code
Mar 22, 2015

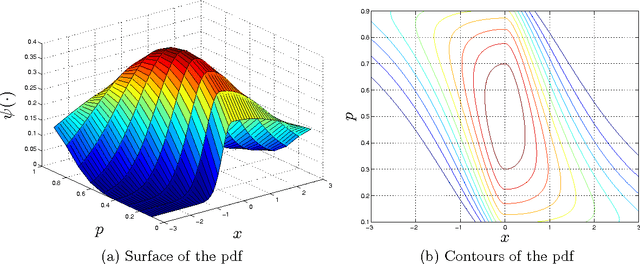
This paper introduces constrained mixtures for continuous distributions, characterized by a mixture of distributions where each distribution has a shape similar to the base distribution and disjoint domains. This new concept is used to create generalized asymmetric versions of the Laplace and normal distributions, which are shown to define exponential families, with known conjugate priors, and to have maximum likelihood estimates for the original parameters, with known closed-form expressions. The asymmetric and symmetric normal distributions are compared in a linear regression example, showing that the asymmetric version performs at least as well as the symmetric one, and in a real world time-series problem, where a hidden Markov model is used to fit a stock index, indicating that the asymmetric version provides higher likelihood and may learn distribution models over states and transition distributions with considerably less entropy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge