Missing Data Estimation in High-Dimensional Datasets: A Swarm Intelligence-Deep Neural Network Approach

In this paper, we examine the problem of missing data in high-dimensional datasets by taking into consideration the Missing Completely at Random and Missing at Random mechanisms, as well as theArbitrary missing pattern. Additionally, this paper employs a methodology based on Deep Learning and Swarm Intelligence algorithms in order to provide reliable estimates for missing data. The deep learning technique is used to extract features from the input data via an unsupervised learning approach by modeling the data distribution based on the input. This deep learning technique is then used as part of the objective function for the swarm intelligence technique in order to estimate the missing data after a supervised fine-tuning phase by minimizing an error function based on the interrelationship and correlation between features in the dataset. The investigated methodology in this paper therefore has longer running times, however, the promising potential outcomes justify the trade-off. Also, basic knowledge of statistics is presumed.

Proposition of a Theoretical Model for Missing Data Imputation using Deep Learning and Evolutionary Algorithms

In the last couple of decades, there has been major advancements in the domain of missing data imputation. The techniques in the domain include amongst others: Expectation Maximization, Neural Networks with Evolutionary Algorithms or optimization techniques and K-Nearest Neighbor approaches to solve the problem. The presence of missing data entries in databases render the tasks of decision-making and data analysis nontrivial. As a result this area has attracted a lot of research interest with the aim being to yield accurate and time efficient and sensitive missing data imputation techniques especially when time sensitive applications are concerned like power plants and winding processes. In this article, considering arbitrary and monotone missing data patterns, we hypothesize that the use of deep neural networks built using autoencoders and denoising autoencoders in conjunction with genetic algorithms, swarm intelligence and maximum likelihood estimator methods as novel data imputation techniques will lead to better imputed values than existing techniques. Also considered are the missing at random, missing completely at random and missing not at random missing data mechanisms. We also intend to use fuzzy logic in tandem with deep neural networks to perform the missing data imputation tasks, as well as different building blocks for the deep neural networks like Stacked Restricted Boltzmann Machines and Deep Belief Networks to test our hypothesis. The motivation behind this article is the need for missing data imputation techniques that lead to better imputed values than existing methods with higher accuracies and lower errors.

Missing Data Prediction and Classification: The Use of Auto-Associative Neural Networks and Optimization Algorithms

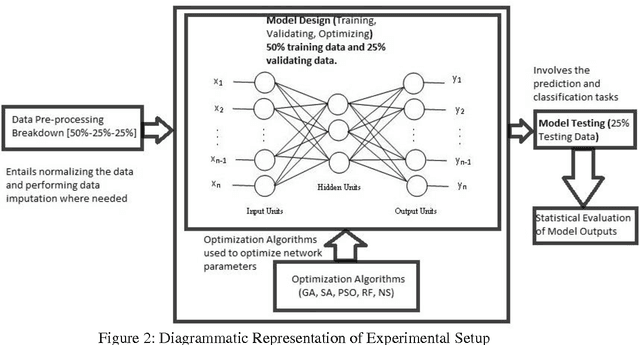
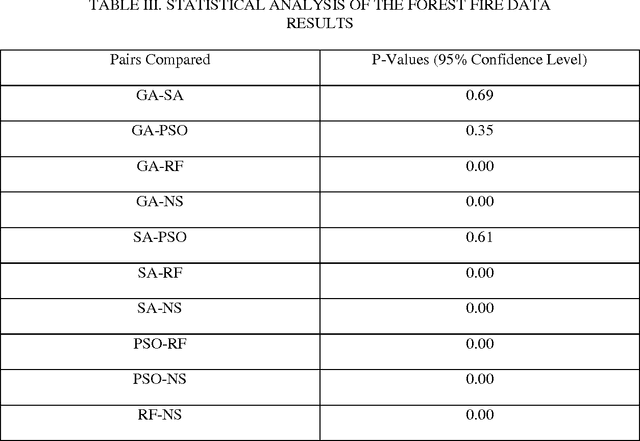
This paper presents methods which are aimed at finding approximations to missing data in a dataset by using optimization algorithms to optimize the network parameters after which prediction and classification tasks can be performed. The optimization methods that are considered are genetic algorithm (GA), simulated annealing (SA), particle swarm optimization (PSO), random forest (RF) and negative selection (NS) and these methods are individually used in combination with auto-associative neural networks (AANN) for missing data estimation and the results obtained are compared. The methods suggested use the optimization algorithms to minimize an error function derived from training the auto-associative neural network during which the interrelationships between the inputs and the outputs are obtained and stored in the weights connecting the different layers of the network. The error function is expressed as the square of the difference between the actual observations and predicted values from an auto-associative neural network. In the event of missing data, all the values of the actual observations are not known hence, the error function is decomposed to depend on the known and unknown variable values. Multi-layer perceptron (MLP) neural network is employed to train the neural networks using the scaled conjugate gradient (SCG) method. Prediction accuracy is determined by mean squared error (MSE), root mean squared error (RMSE), mean absolute error (MAE), and correlation coefficient (r) computations. Accuracy in classification is obtained by plotting ROC curves and calculating the areas under these. Analysis of results depicts that the approach using RF with AANN produces the most accurate predictions and classifications while on the other end of the scale is the approach which entails using NS with AANN.