On the Computational Tractability of the (Many) Shapley Values

Recent studies have examined the computational complexity of computing Shapley additive explanations (also known as SHAP) across various models and distributions, revealing their tractability or intractability in different settings. However, these studies primarily focused on a specific variant called Conditional SHAP, though many other variants exist and address different limitations. In this work, we analyze the complexity of computing a much broader range of such variants, including Conditional, Interventional, and Baseline SHAP, while exploring both local and global computations. We show that both local and global Interventional and Baseline SHAP can be computed in polynomial time for various ML models under Hidden Markov Model distributions, extending popular algorithms such as TreeSHAP beyond empirical distributions. On the downside, we prove intractability results for these variants over a wide range of neural networks and tree ensembles. We believe that our results emphasize the intricate diversity of computing Shapley values, demonstrating how their complexity is substantially shaped by both the specific SHAP variant, the model type, and the distribution.

Distance and Equivalence between Finite State Machines and Recurrent Neural Networks: Computational results

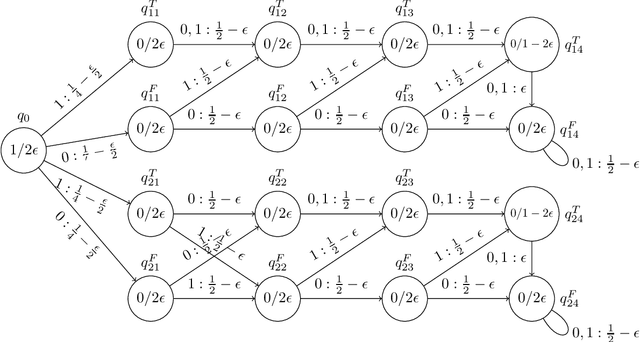
The need of interpreting Deep Learning (DL) models has led, during the past years, to a proliferation of works concerned by this issue. Among strategies which aim at shedding some light on how information is represented internally in DL models, one consists in extracting symbolic rule-based machines from connectionist models that are supposed to approximate well their behaviour. In order to better understand how reasonable these approximation strategies are, we need to know the computational complexity of measuring the quality of approximation. In this article, we will prove some computational results related to the problem of extracting Finite State Machine (FSM) based models from trained RNN Language models. More precisely, we'll show the following: (a) For general weighted RNN-LMs with a single hidden layer and a ReLu activation: - The equivalence problem of a PDFA/PFA/WFA and a weighted first-order RNN-LM is undecidable; - As a corollary, the distance problem between languages generated by PDFA/PFA/WFA and that of a weighted RNN-LM is not recursive; -The intersection between a DFA and the cut language of a weighted RNN-LM is undecidable; - The equivalence of a PDFA/PFA/WFA and weighted RNN-LM in a finite support is EXP-Hard; (b) For consistent weight RNN-LMs with any computable activation function: - The Tcheybechev distance approximation is decidable; - The Tcheybechev distance approximation in a finite support is NP-Hard. Moreover, our reduction technique from 3-SAT makes this latter fact easily generalizable to other RNN architectures (e.g. LSTMs/RNNs), and RNNs with finite precision.

A Canonical Semi-Deterministic Transducer

We prove the existence of a canonical form for semi-deterministic transducers with incomparable sets of output strings. Based on this, we develop an algorithm which learns semi-deterministic transducers given access to translation queries. We also prove that there is no learning algorithm for semi-deterministic transducers that uses only domain knowledge.