Aiding Medical Diagnosis Through the Application of Graph Neural Networks to Functional MRI Scans

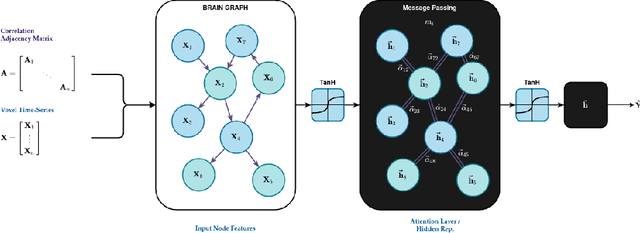
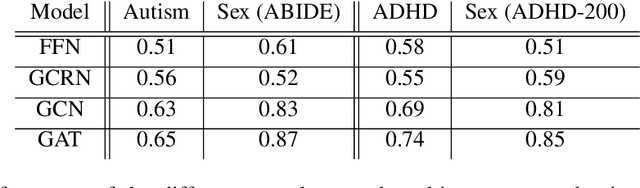
Graph Neural Networks (GNNs) have been shown to be a powerful tool for generating predictions from biological data. Their application to neuroimaging data such as functional magnetic resonance imaging (fMRI) scans has been limited. However, applying GNNs to fMRI scans may substantially improve predictive accuracy and could be used to inform clinical diagnosis in the future. In this paper, we present a novel approach to representing resting-state fMRI data as a graph containing nodes and edges without omitting any of the voxels and thus reducing information loss. We compare multiple GNN architectures and show that they can successfully predict the disease and sex of a person. We hope to provide a basis for future work to exploit the power of GNNs when applied to brain imaging data.

Continuous-Depth Neural Models for Dynamic Graph Prediction

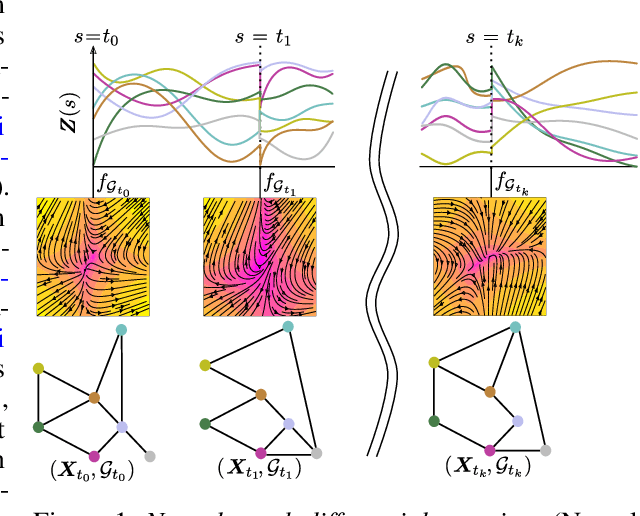
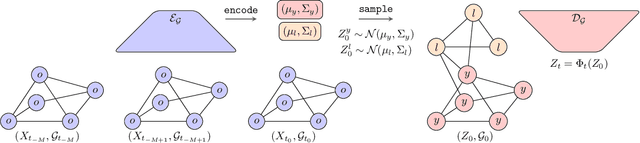
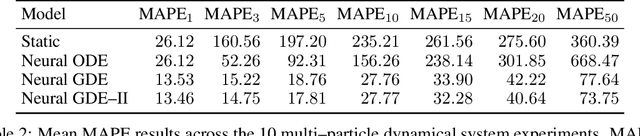
We introduce the framework of continuous-depth graph neural networks (GNNs). Neural graph differential equations (Neural GDEs) are formalized as the counterpart to GNNs where the input-output relationship is determined by a continuum of GNN layers, blending discrete topological structures and differential equations. The proposed framework is shown to be compatible with static GNN models and is extended to dynamic and stochastic settings through hybrid dynamical system theory. Here, Neural GDEs improve performance by exploiting the underlying dynamics geometry, further introducing the ability to accommodate irregularly sampled data. Results prove the effectiveness of the proposed models across applications, such as traffic forecasting or prediction in genetic regulatory networks.