Claudio Lucio do Val Lopes
Analyzing Dominance Move (MIP-DoM) Indicator for Multi- and Many-objective Optimization
Dec 22, 2020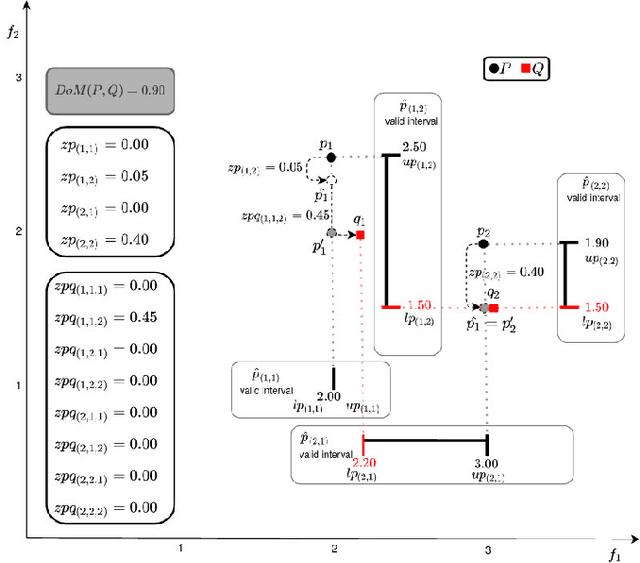
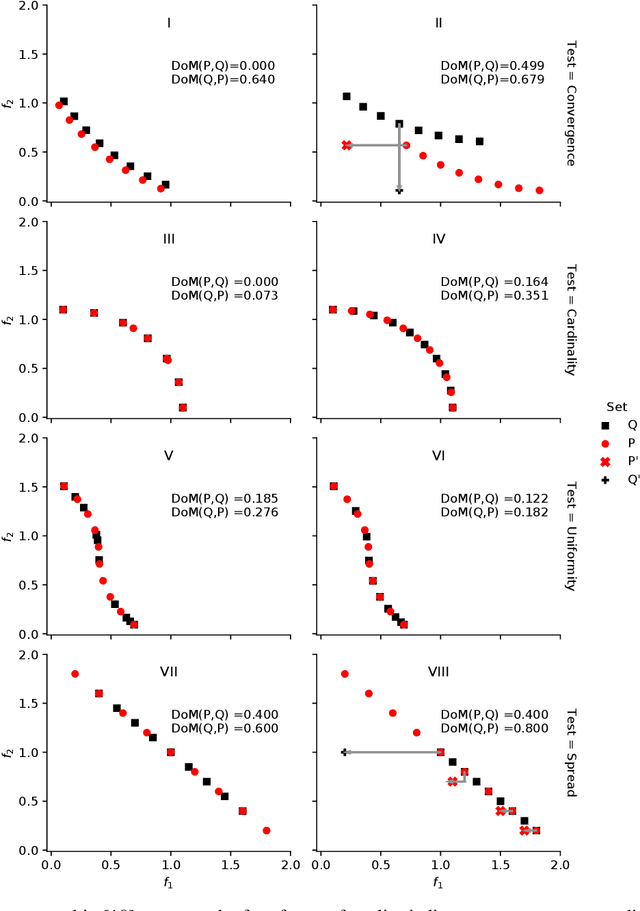

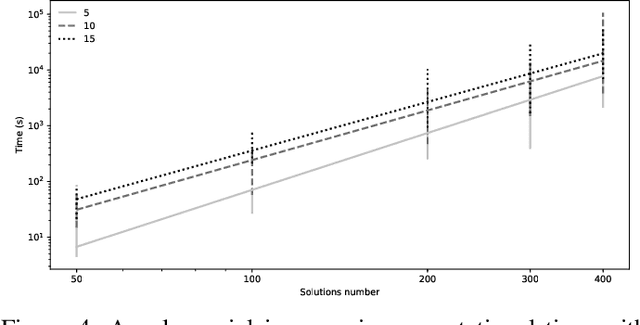
Abstract:Dominance move (DoM) is a binary quality indicator that can be used in multi-objective and many-objective optimization to compare two solution sets obtained from different algorithms. The DoM indicator can differentiate the sets for certain important features, such as convergence, spread, uniformity, and cardinality. The DoM indicator has an intuitive and physical meaning, similar to the $\epsilon$-indicator, and calculates the minimum total move of members of one set needed to weakly dominate each member of the other set. Despite the aforementioned properties, DoM is hard to calculate, particularly in higher dimensions. There is an efficient and exact method to calculate it in a bi-objective case only. This work proposes a novel approach to calculate DoM using a mixed integer programming (MIP) approach, which can handle sets with three or more objectives and is shown to overcome the $\epsilon$-indicator's information loss. Experiments, in the bi-objective space, are done to verify the model's correctness. Furthermore, other experiments, using 3, 5, 10, 15, 20, 25 and 30-objective problems are performed to show how the model behaves in higher-dimensional cases. Algorithms, such as IBEA, MOEA/D, NSGA-III, NSGA-II, and SPEA2 are used to generate the solution sets (however any other algorithms can also be used with the proposed MIP-DoM indicator). Further extensions are discussed to handle certain idiosyncrasies with some solution sets and also to improve the quality indicator and its use for other situations.
An Assignment Problem Formulation for Dominance Move Indicator
Feb 25, 2020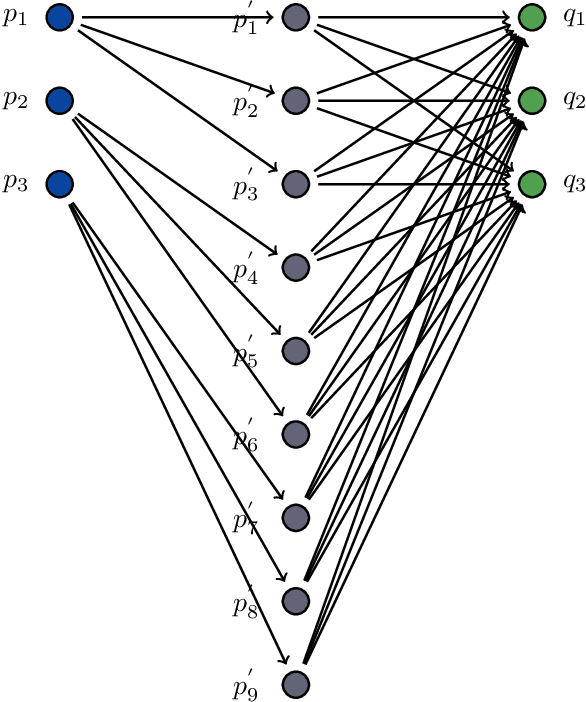
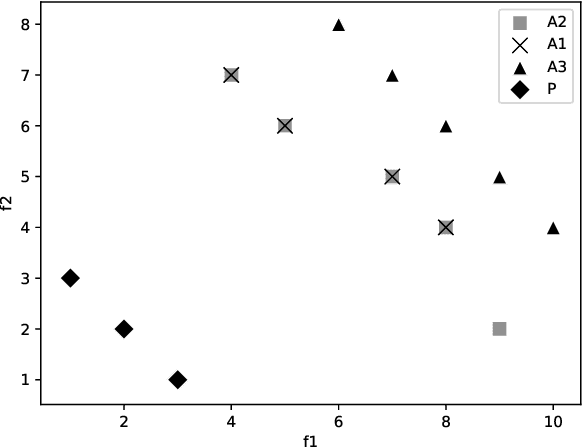
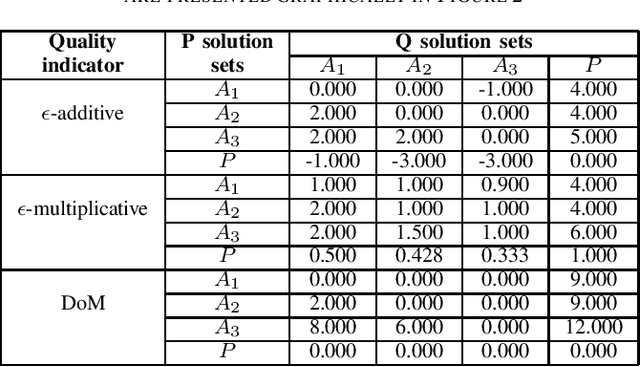
Abstract:Dominance move (DoM) is a binary quality indicator to compare solution sets in multiobjective optimization. The indicator allows a more natural and intuitive relation when comparing solution sets. It is Pareto compliant and does not demand any parameters or reference sets. In spite of its advantages, the combinatorial calculation nature is a limitation. The original formulation presents an efficient method to calculate it in a biobjective case only. This work presents an assignment formulation to calculate DoM in problems with three objectives or more. Some initial experiments, in the biobjective space, were done to present the model correctness. Next, other experiments, using three dimensions, were also done to show how DoM could be compared with other indicators: inverted generational distance (IGD) and hypervolume (HV). Results show the assignment formulation for DoM is valid for more than three objectives. However, there are some strengths and weaknesses, which are discussed and detailed. Some notes, considerations, and future research paths conclude this work.
Dominance Move calculation using a MIP approach for comparison of multi and many-objective optimization solution sets
Jan 10, 2020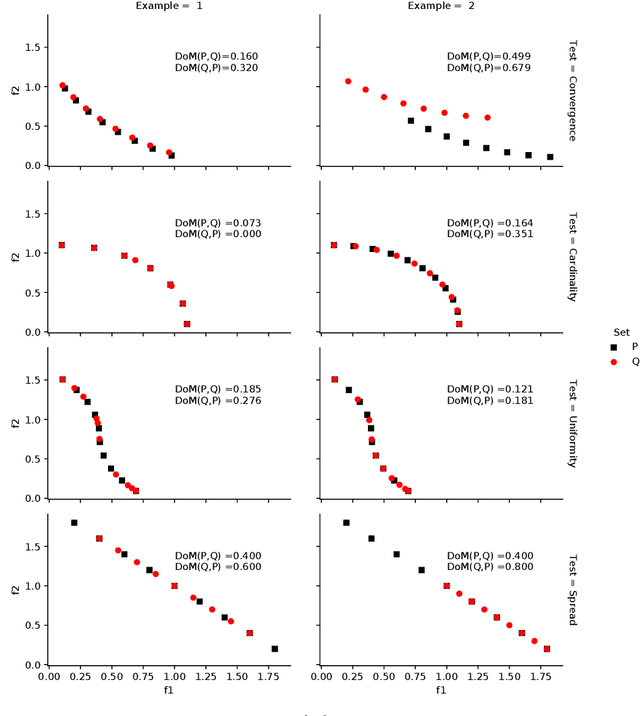
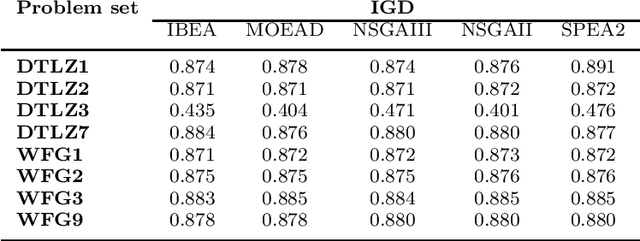

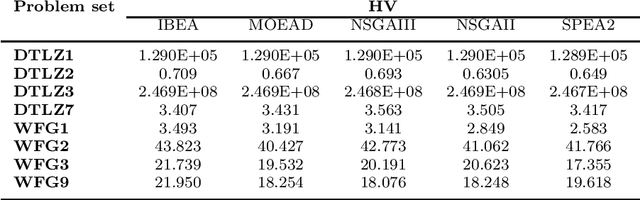
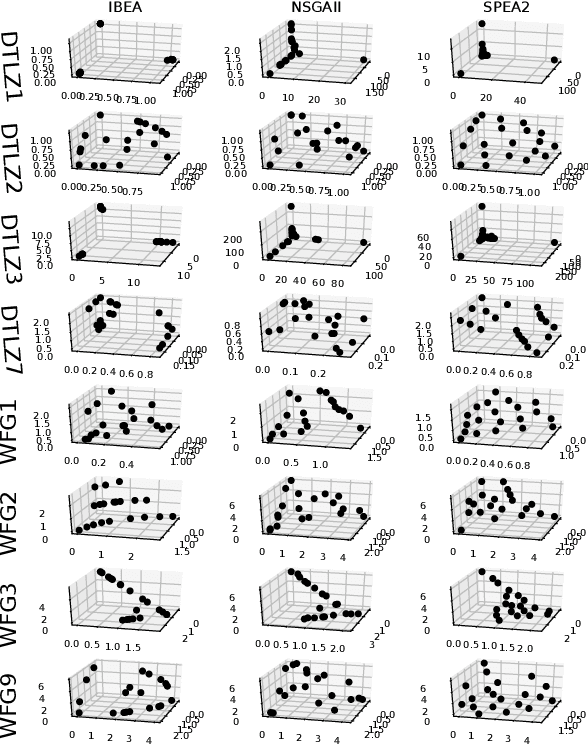
Abstract:Dominance move (DoM) is a binary quality indicator that can be used in multiobjective optimization. It can compare solution sets while representing some important features such as convergence, spread, uniformity, and cardinality. DoM has an intuitive concept and considers the minimum move of one set needed to weakly Pareto dominate the other set. Despite the aforementioned properties, DoM is hard to calculate. The original formulation presents an efficient and exact method to calculate it in a biobjective case only. This work presents a new approach to calculate and extend DoM to deal with three or more objectives. The idea is to use a mixed integer programming (MIP) approach to calculate DoM. Some initial experiments, in the biobjective space, were done to verify the model correctness. Furthermore, other experiments, using three, five, and ten objective functions were done to show how the model behaves in higher dimensional cases. Algorithms such as IBEA, MOEAD, NSGAIII, NSGAII, and SPEA2 were used to generate the solution sets, however any other algorithms could be used with DoM indicator. The results have confirmed the effectiveness of the MIP DoM in problems with more than three objective functions. Final notes, considerations, and future research are discussed to exploit some solution sets particularities and improve the model and its use for other situations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge