An Assignment Problem Formulation for Dominance Move Indicator

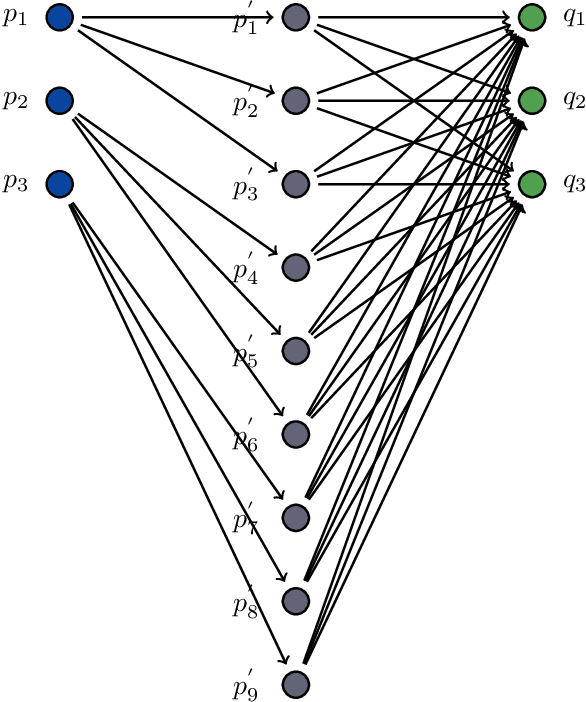
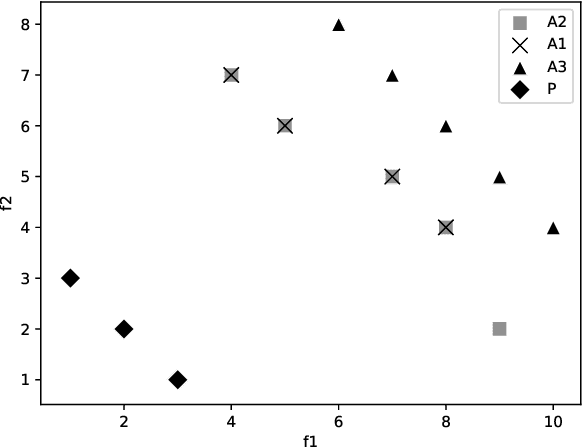
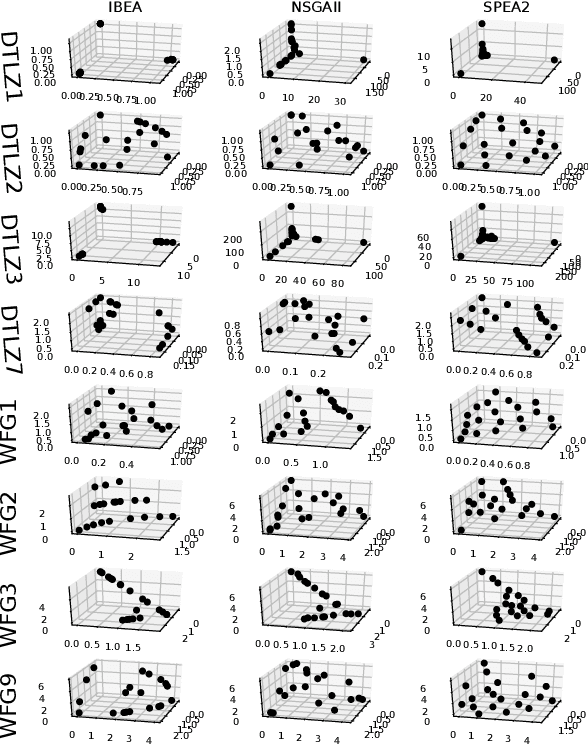
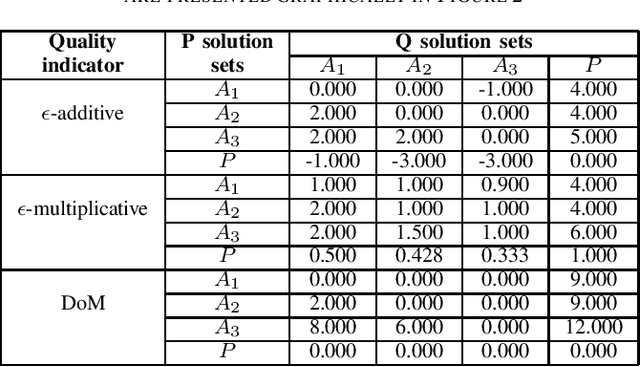
Dominance move (DoM) is a binary quality indicator to compare solution sets in multiobjective optimization. The indicator allows a more natural and intuitive relation when comparing solution sets. It is Pareto compliant and does not demand any parameters or reference sets. In spite of its advantages, the combinatorial calculation nature is a limitation. The original formulation presents an efficient method to calculate it in a biobjective case only. This work presents an assignment formulation to calculate DoM in problems with three objectives or more. Some initial experiments, in the biobjective space, were done to present the model correctness. Next, other experiments, using three dimensions, were also done to show how DoM could be compared with other indicators: inverted generational distance (IGD) and hypervolume (HV). Results show the assignment formulation for DoM is valid for more than three objectives. However, there are some strengths and weaknesses, which are discussed and detailed. Some notes, considerations, and future research paths conclude this work.

Sample size calculations for the experimental comparison of multiple algorithms on multiple problem instances

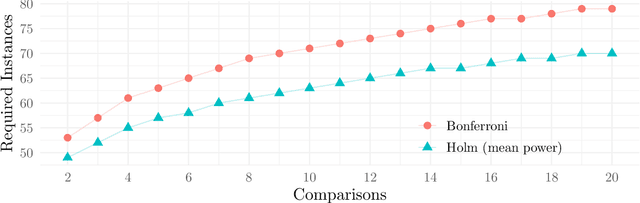
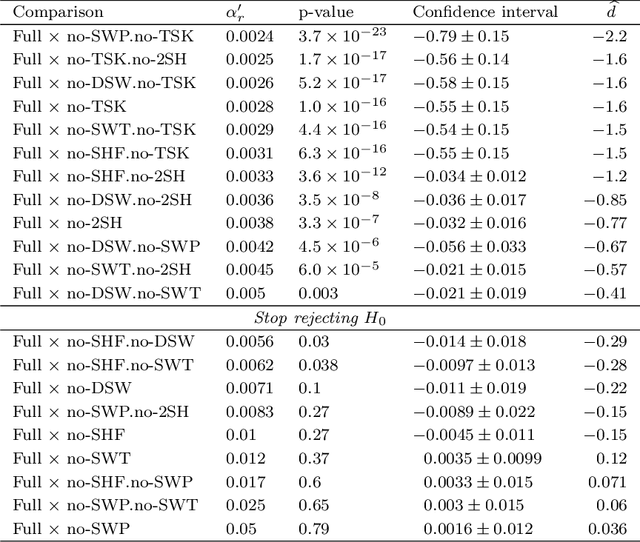
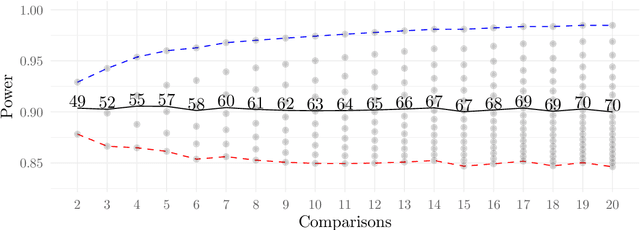
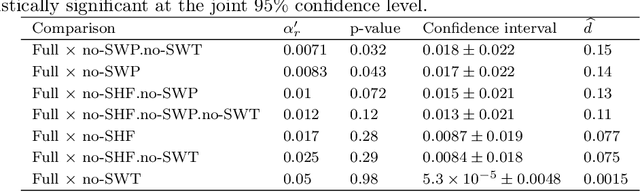
This work presents a statistically principled method for estimating the required number of instances in the experimental comparison of multiple algorithms on a given problem class of interest. This approach generalises earlier results by allowing researchers to design experiments based on the desired best, worst, mean or median-case statistical power to detect differences between algorithms larger than a certain threshold. Holm's step-down procedure is used to maintain the overall significance level controlled at desired levels, without resulting in overly conservative experiments. This paper also presents an approach for sampling each algorithm on each instance, based on optimal sample size ratios that minimise the total required number of runs subject to a desired accuracy in the estimation of paired differences. A case study investigating the effect of 21 variants of a custom-tailored Simulated Annealing for a class of scheduling problems is used to illustrate the application of the proposed methods for sample size calculations in the experimental comparison of algorithms.