Sample size calculations for the experimental comparison of multiple algorithms on multiple problem instances
Paper and Code
Aug 05, 2019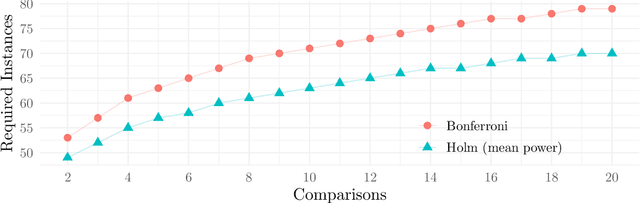
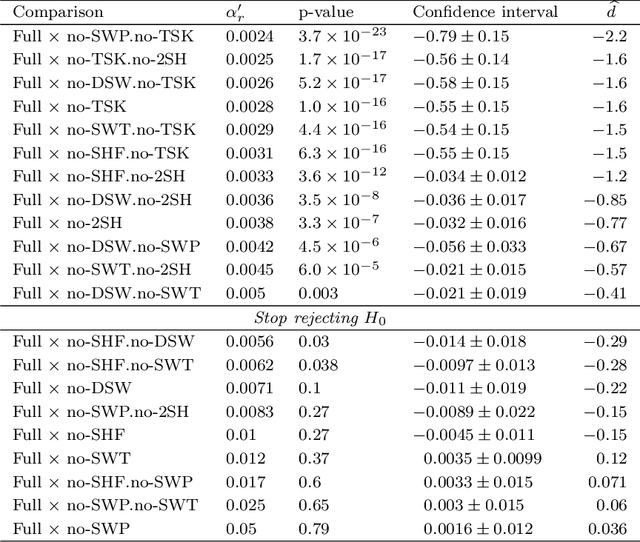
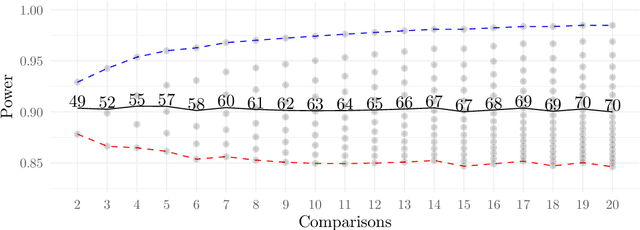
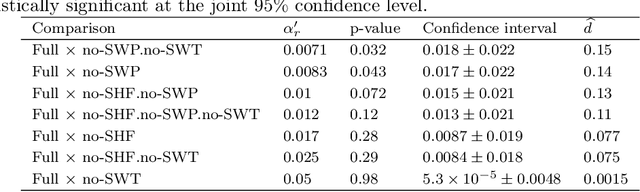
This work presents a statistically principled method for estimating the required number of instances in the experimental comparison of multiple algorithms on a given problem class of interest. This approach generalises earlier results by allowing researchers to design experiments based on the desired best, worst, mean or median-case statistical power to detect differences between algorithms larger than a certain threshold. Holm's step-down procedure is used to maintain the overall significance level controlled at desired levels, without resulting in overly conservative experiments. This paper also presents an approach for sampling each algorithm on each instance, based on optimal sample size ratios that minimise the total required number of runs subject to a desired accuracy in the estimation of paired differences. A case study investigating the effect of 21 variants of a custom-tailored Simulated Annealing for a class of scheduling problems is used to illustrate the application of the proposed methods for sample size calculations in the experimental comparison of algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge