Dominance Move calculation using a MIP approach for comparison of multi and many-objective optimization solution sets
Paper and Code
Jan 10, 2020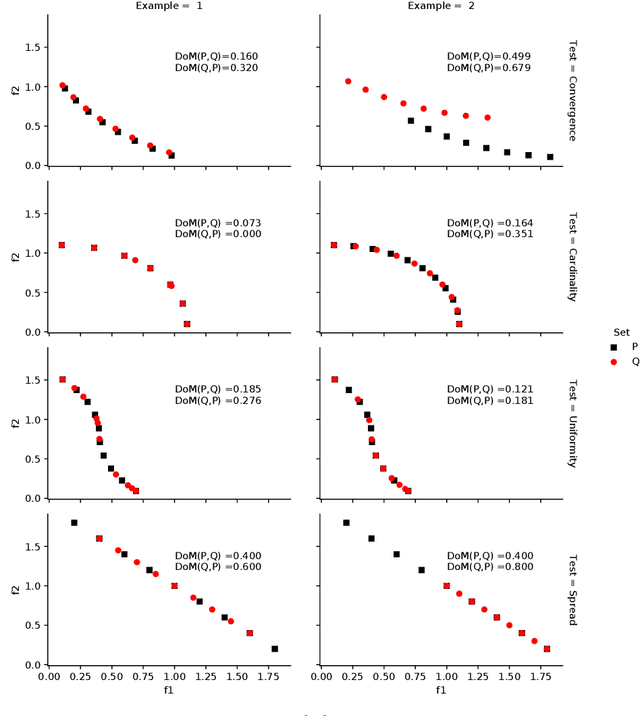
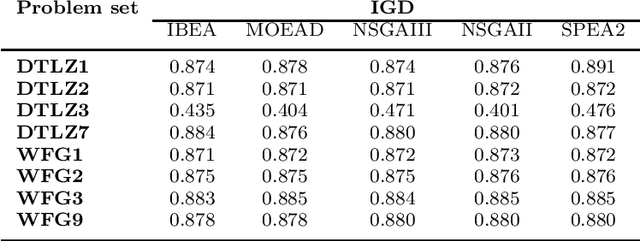

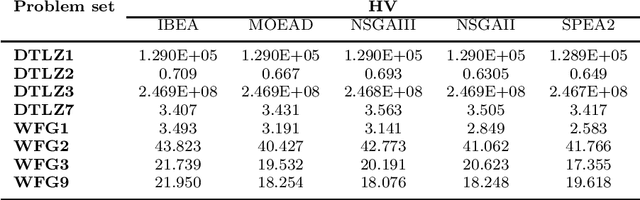
Dominance move (DoM) is a binary quality indicator that can be used in multiobjective optimization. It can compare solution sets while representing some important features such as convergence, spread, uniformity, and cardinality. DoM has an intuitive concept and considers the minimum move of one set needed to weakly Pareto dominate the other set. Despite the aforementioned properties, DoM is hard to calculate. The original formulation presents an efficient and exact method to calculate it in a biobjective case only. This work presents a new approach to calculate and extend DoM to deal with three or more objectives. The idea is to use a mixed integer programming (MIP) approach to calculate DoM. Some initial experiments, in the biobjective space, were done to verify the model correctness. Furthermore, other experiments, using three, five, and ten objective functions were done to show how the model behaves in higher dimensional cases. Algorithms such as IBEA, MOEAD, NSGAIII, NSGAII, and SPEA2 were used to generate the solution sets, however any other algorithms could be used with DoM indicator. The results have confirmed the effectiveness of the MIP DoM in problems with more than three objective functions. Final notes, considerations, and future research are discussed to exploit some solution sets particularities and improve the model and its use for other situations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge