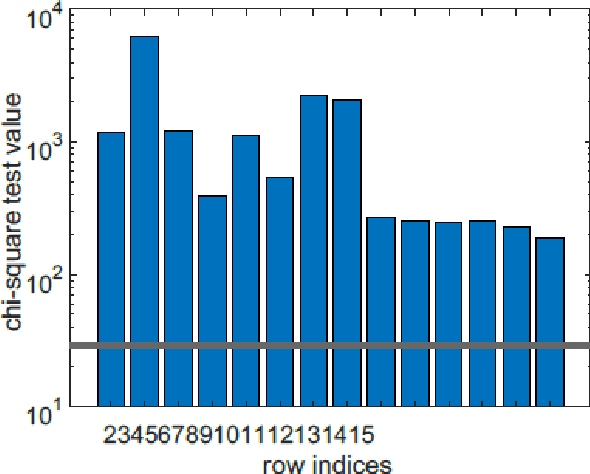
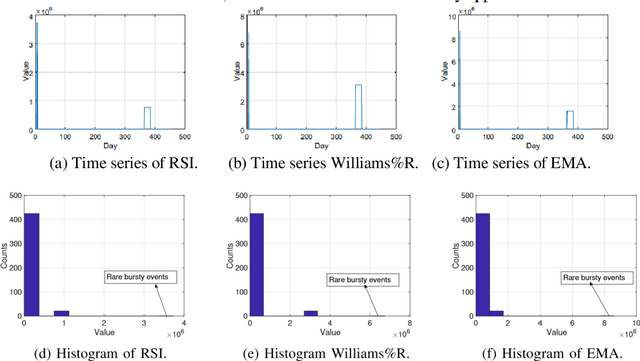
Improving CNN-base Stock Trading By Considering Data Heterogeneity and Burst

In recent years, there have been quite a few attempts to apply intelligent techniques to financial trading, i.e., constructing automatic and intelligent trading framework based on historical stock price. Due to the unpredictable, uncertainty and volatile nature of financial market, researchers have also resorted to deep learning to construct the intelligent trading framework. In this paper, we propose to use CNN as the core functionality of such framework, because it is able to learn the spatial dependency (i.e., between rows and columns) of the input data. However, different with existing deep learning-based trading frameworks, we develop novel normalization process to prepare the stock data. In particular, we first empirically observe that the stock data is intrinsically heterogeneous and bursty, and then validate the heterogeneity and burst nature of stock data from a statistical perspective. Next, we design the data normalization method in a way such that the data heterogeneity is preserved and bursty events are suppressed. We verify out developed CNN-based trading framework plus our new normalization method on 29 stocks. Experiment results show that our approach can outperform other comparing approaches.

Quantum-Inspired Classical Algorithm for Principal Component Regression

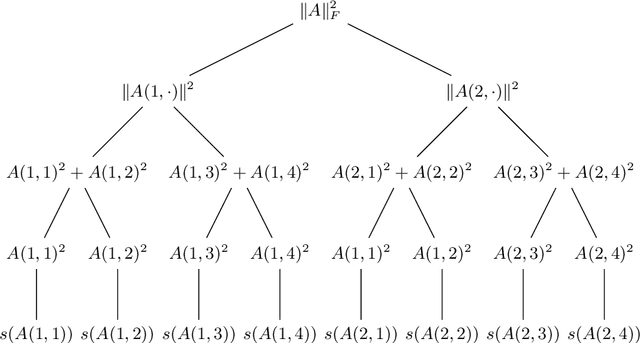
This paper presents a sublinear classical algorithm for principal component regression. The algorithm uses quantum-inspired linear algebra, an idea developed by Tang. Using this technique, her algorithm for recommendation systems achieved runtime only polynomially slower than its quantum counterpart. Her work was quickly adapted to solve many other problems in sublinear time complexity. In this work, we developed an algorithm for principal component regression that runs in time polylogarithmic to the number of data points, an exponential speed up over the state-of-the-art algorithm, under the mild assumption that the input is given in some data structure that supports a norm-based sampling procedure. This exponential speed up allows for potential applications in much larger data sets.