Partitioning Distributed Compute Jobs with Reinforcement Learning and Graph Neural Networks

From natural language processing to genome sequencing, large-scale machine learning models are bringing advances to a broad range of fields. Many of these models are too large to be trained on a single machine, and instead must be distributed across multiple devices. This has motivated the research of new compute and network systems capable of handling such tasks. In particular, recent work has focused on developing management schemes which decide how to allocate distributed resources such that some overall objective, such as minimising the job completion time (JCT), is optimised. However, such studies omit explicit consideration of how much a job should be distributed, usually assuming that maximum distribution is desirable. In this work, we show that maximum parallelisation is sub-optimal in relation to user-critical metrics such as throughput and blocking rate. To address this, we propose PAC-ML (partitioning for asynchronous computing with machine learning). PAC-ML leverages a graph neural network and reinforcement learning to learn how much to partition computation graphs such that the number of jobs which meet arbitrary user-defined JCT requirements is maximised. In experiments with five real deep learning computation graphs on a recently proposed optical architecture across four user-defined JCT requirement distributions, we demonstrate PAC-ML achieving up to 56.2% lower blocking rates in dynamic job arrival settings than the canonical maximum parallelisation strategy used by most prior works.

Reinforcement Learning for Branch-and-Bound Optimisation using Retrospective Trajectories

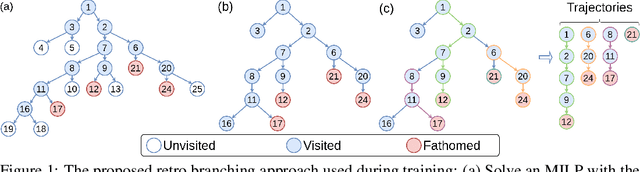
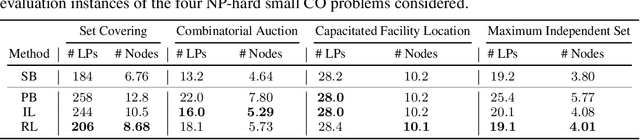
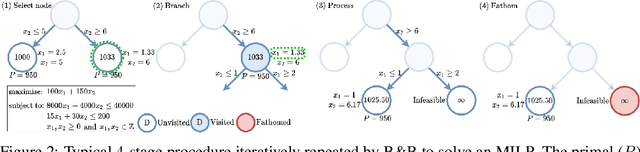
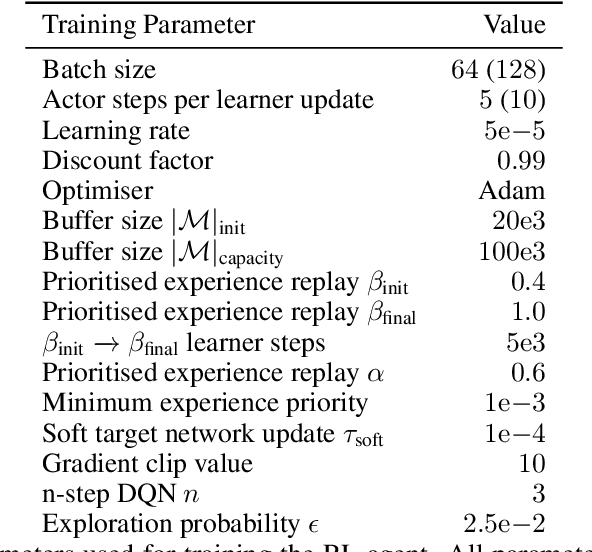
Combinatorial optimisation problems framed as mixed integer linear programmes (MILPs) are ubiquitous across a range of real-world applications. The canonical branch-and-bound (B&B) algorithm seeks to exactly solve MILPs by constructing a search tree of increasingly constrained sub-problems. In practice, its solving time performance is dependent on heuristics, such as the choice of the next variable to constrain ('branching'). Recently, machine learning (ML) has emerged as a promising paradigm for branching. However, prior works have struggled to apply reinforcement learning (RL), citing sparse rewards, difficult exploration, and partial observability as significant challenges. Instead, leading ML methodologies resort to approximating high quality handcrafted heuristics with imitation learning (IL), which precludes the discovery of novel policies and requires expensive data labelling. In this work, we propose retro branching; a simple yet effective approach to RL for branching. By retrospectively deconstructing the search tree into multiple paths each contained within a sub-tree, we enable the agent to learn from shorter trajectories with more predictable next states. In experiments on four combinatorial tasks, our approach enables learning-to-branch without any expert guidance or pre-training. We outperform the current state-of-the-art RL branching algorithm by 3-5x and come within 20% of the best IL method's performance on MILPs with 500 constraints and 1000 variables, with ablations verifying that our retrospectively constructed trajectories are essential to achieving these results.

Learning to Solve Combinatorial Graph Partitioning Problems via Efficient Exploration

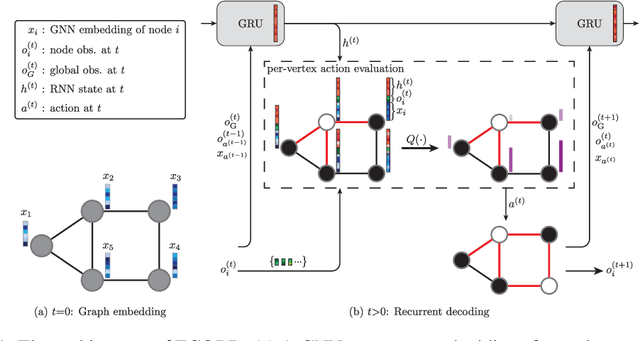
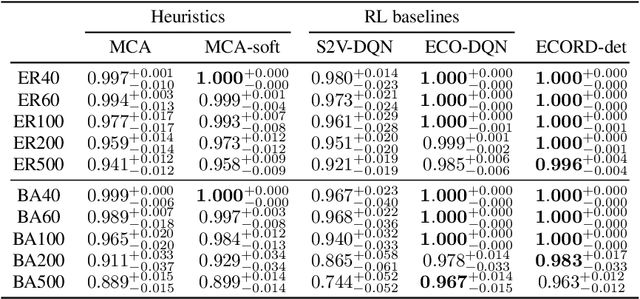
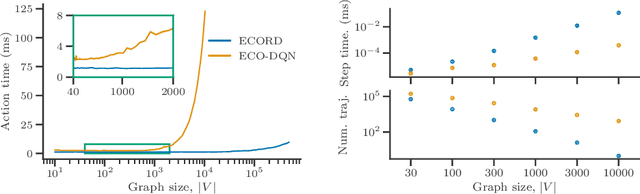
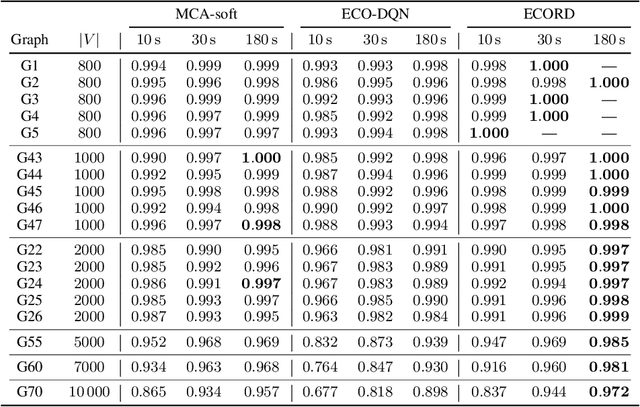
From logistics to the natural sciences, combinatorial optimisation on graphs underpins numerous real-world applications. Reinforcement learning (RL) has shown particular promise in this setting as it can adapt to specific problem structures and does not require pre-solved instances for these, often NP-hard, problems. However, state-of-the-art (SOTA) approaches typically suffer from severe scalability issues, primarily due to their reliance on expensive graph neural networks (GNNs) at each decision step. We introduce ECORD; a novel RL algorithm that alleviates this expense by restricting the GNN to a single pre-processing step, before entering a fast-acting exploratory phase directed by a recurrent unit. Experimentally, ECORD achieves a new SOTA for RL algorithms on the Maximum Cut problem, whilst also providing orders of magnitude improvement in speed and scalability. Compared to the nearest competitor, ECORD reduces the optimality gap by up to 73% on 500 vertex graphs with a decreased wall-clock time. Moreover, ECORD retains strong performance when generalising to larger graphs with up to 10000 vertices.