Mechanistic Interpretability and Causal Feature Steering of Neural Quantum States via Sparse Autoencoders

Neural Quantum States (NQS) are a remarkably expressive class of variational ansätze for quantum many-body wavefunctions, yet little is understood about their internal mechanisms: trained on variational objectives alone, how do NQS accurately capture physical observables that they have never been explicitly optimized for? In this work, we present a systematic approach to analyze the internal activations of NQS using sparse autoencoders. We extract features from the residual stream and demonstrate that these features strongly correlate with physical observables such as order parameters, staggered magnetization, and half-chain correlators, across both ground state representation and real-time dynamics. Remarkably, the discovery of these features is entirely unsupervised, with no physical labels provided. We further establish that such features causally affect the corresponding observables predicted by NQS, by showing that targeted, post-training intervention on a \textit{single} feature smoothly and monotonically steers the corresponding observable, while leaving the variational energy nearly unchanged. These results demonstrate that NQS are not merely functional approximators, but encode rich, interpretable internal representations of physical information. Our approach provides both a diagnostic and an intervention tool for NQS, and serves as a foundation for using mechanistic interpretability towards more reliable, transparent NQS.

chebgreen: Learning and Interpolating Continuous Empirical Green's Functions from Data

In this work, we present a mesh-independent, data-driven library, chebgreen, to mathematically model one-dimensional systems, possessing an associated control parameter, and whose governing partial differential equation is unknown. The proposed method learns an Empirical Green's Function for the associated, but hidden, boundary value problem, in the form of a Rational Neural Network from which we subsequently construct a bivariate representation in a Chebyshev basis. We uncover the Green's function, at an unseen control parameter value, by interpolating the left and right singular functions within a suitable library, expressed as points on a manifold of Quasimatrices, while the associated singular values are interpolated with Lagrange polynomials.

Weak-PDE-LEARN: A Weak Form Based Approach to Discovering PDEs From Noisy, Limited Data

We introduce Weak-PDE-LEARN, a Partial Differential Equation (PDE) discovery algorithm that can identify non-linear PDEs from noisy, limited measurements of their solutions. Weak-PDE-LEARN uses an adaptive loss function based on weak forms to train a neural network, $U$, to approximate the PDE solution while simultaneously identifying the governing PDE. This approach yields an algorithm that is robust to noise and can discover a range of PDEs directly from noisy, limited measurements of their solutions. We demonstrate the efficacy of Weak-PDE-LEARN by learning several benchmark PDEs.

PDE-LEARN: Using Deep Learning to Discover Partial Differential Equations from Noisy, Limited Data

In this paper, we introduce PDE-LEARN, a novel PDE discovery algorithm that can identify governing partial differential equations (PDEs) directly from noisy, limited measurements of a physical system of interest. PDE-LEARN uses a Rational Neural Network, $U$, to approximate the system response function and a sparse, trainable vector, $\xi$, to characterize the hidden PDE that the system response function satisfies. Our approach couples the training of $U$ and $\xi$ using a loss function that (1) makes $U$ approximate the system response function, (2) encapsulates the fact that $U$ satisfies a hidden PDE that $\xi$ characterizes, and (3) promotes sparsity in $\xi$ using ideas from iteratively reweighted least-squares. Further, PDE-LEARN can simultaneously learn from several data sets, allowing it to incorporate results from multiple experiments. This approach yields a robust algorithm to discover PDEs directly from realistic scientific data. We demonstrate the efficacy of PDE-LEARN by identifying several PDEs from noisy and limited measurements.

PDE-READ: Human-readable Partial Differential Equation Discovery using Deep Learning

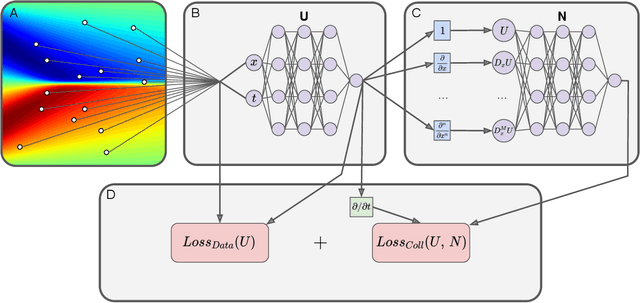
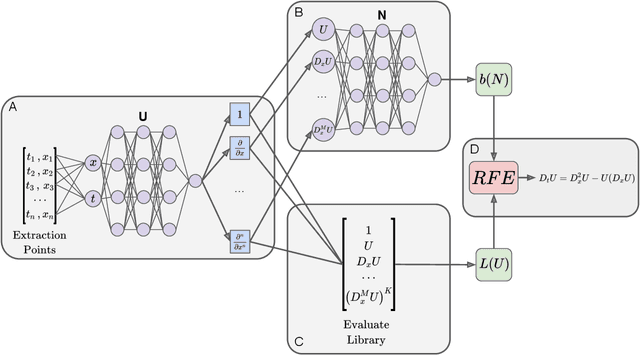
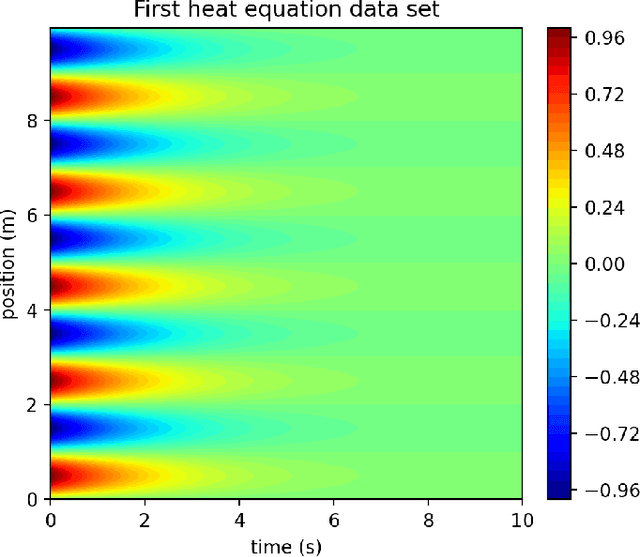
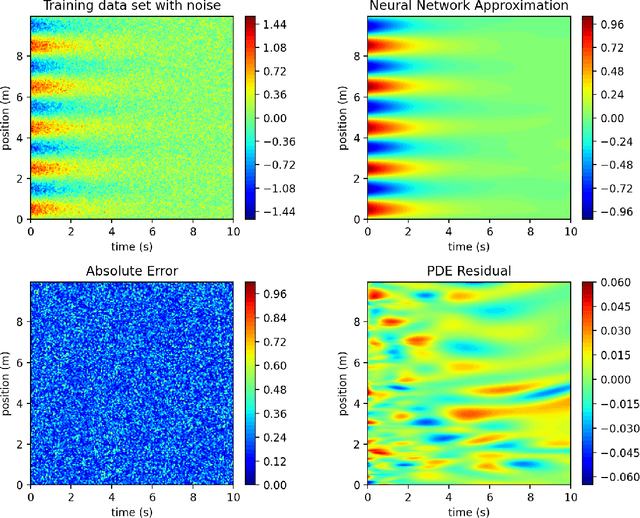
PDE discovery shows promise for uncovering predictive models for complex physical systems but has difficulty when measurements are sparse and noisy. We introduce a new approach for PDE discovery that uses two Rational Neural Networks and a principled sparse regression algorithm to identify the hidden dynamics that govern a system's response. The first network learns the system response function, while the second learns a hidden PDE which drives the system's evolution. We then use a parameter-free sparse regression algorithm to extract a human-readable form of the hidden PDE from the second network. We implement our approach in an open-source library called PDE-READ. Our approach successfully identifies the Heat, Burgers, and Korteweg-De Vries equations with remarkable consistency. We demonstrate that our approach is unprecedentedly robust to both sparsity and noise and is, therefore, applicable to real-world observational data.