PDE-READ: Human-readable Partial Differential Equation Discovery using Deep Learning

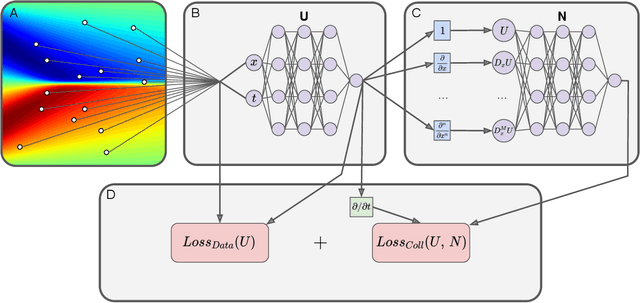
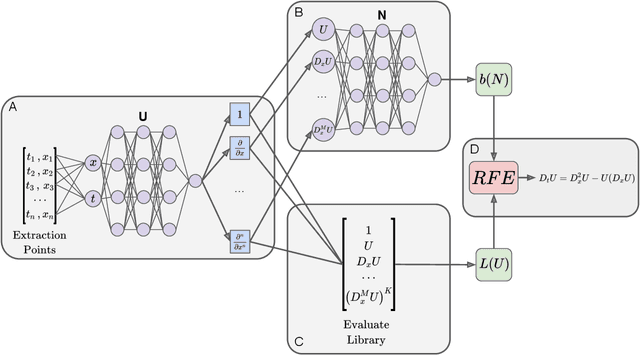
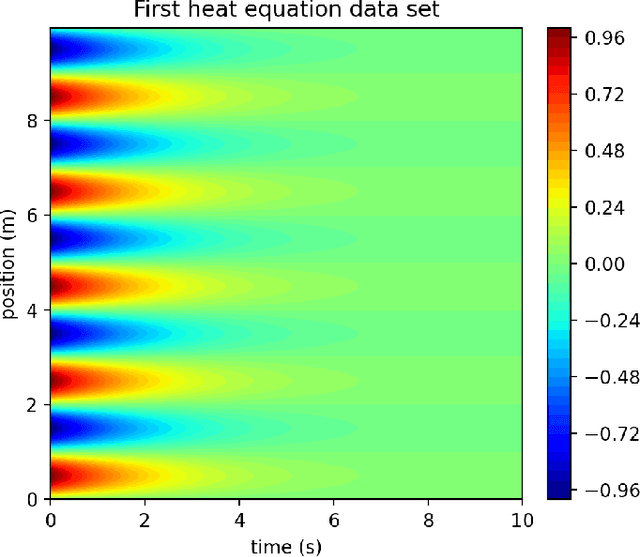
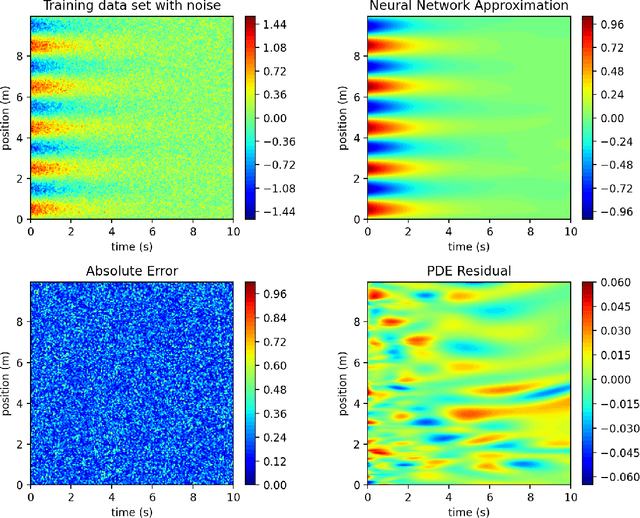
PDE discovery shows promise for uncovering predictive models for complex physical systems but has difficulty when measurements are sparse and noisy. We introduce a new approach for PDE discovery that uses two Rational Neural Networks and a principled sparse regression algorithm to identify the hidden dynamics that govern a system's response. The first network learns the system response function, while the second learns a hidden PDE which drives the system's evolution. We then use a parameter-free sparse regression algorithm to extract a human-readable form of the hidden PDE from the second network. We implement our approach in an open-source library called PDE-READ. Our approach successfully identifies the Heat, Burgers, and Korteweg-De Vries equations with remarkable consistency. We demonstrate that our approach is unprecedentedly robust to both sparsity and noise and is, therefore, applicable to real-world observational data.