PDE-LEARN: Using Deep Learning to Discover Partial Differential Equations from Noisy, Limited Data

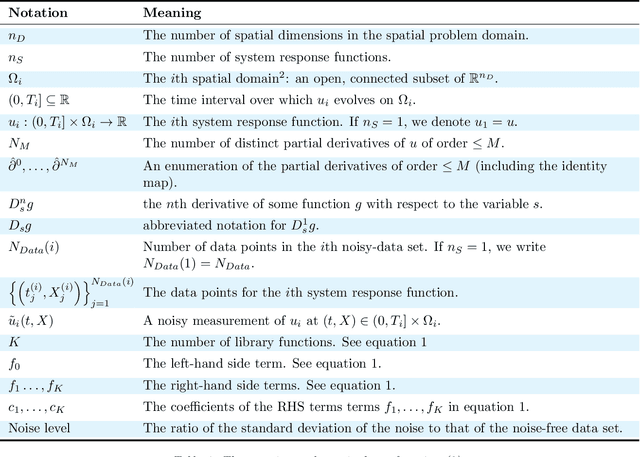
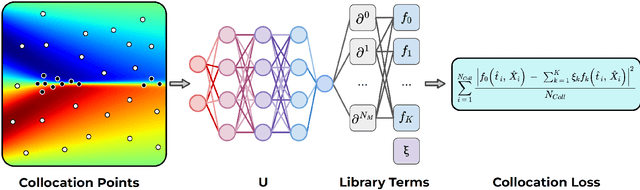
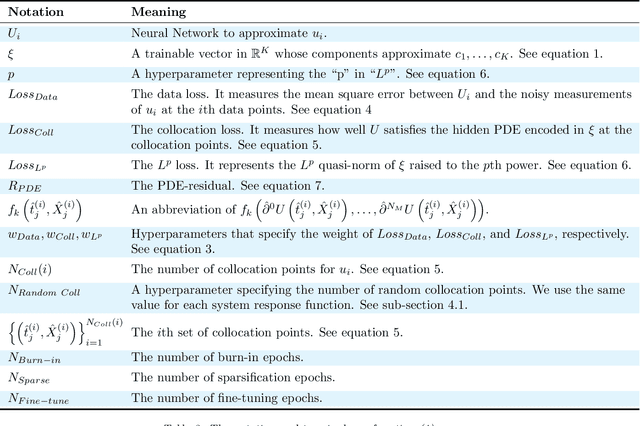
In this paper, we introduce PDE-LEARN, a novel PDE discovery algorithm that can identify governing partial differential equations (PDEs) directly from noisy, limited measurements of a physical system of interest. PDE-LEARN uses a Rational Neural Network, $U$, to approximate the system response function and a sparse, trainable vector, $\xi$, to characterize the hidden PDE that the system response function satisfies. Our approach couples the training of $U$ and $\xi$ using a loss function that (1) makes $U$ approximate the system response function, (2) encapsulates the fact that $U$ satisfies a hidden PDE that $\xi$ characterizes, and (3) promotes sparsity in $\xi$ using ideas from iteratively reweighted least-squares. Further, PDE-LEARN can simultaneously learn from several data sets, allowing it to incorporate results from multiple experiments. This approach yields a robust algorithm to discover PDEs directly from realistic scientific data. We demonstrate the efficacy of PDE-LEARN by identifying several PDEs from noisy and limited measurements.