A review of handcrafted and deep radiomics in neurological diseases: transitioning from oncology to clinical neuroimaging

Medical imaging technologies have undergone extensive development, enabling non-invasive visualization of clinical information. The traditional review of medical images by clinicians remains subjective, time-consuming, and prone to human error. With the recent availability of medical imaging data, quantification have become important goals in the field. Radiomics, a methodology aimed at extracting quantitative information from imaging data, has emerged as a promising approach to uncover hidden biological information and support decision-making in clinical practice. This paper presents a review of the radiomic pipeline from the clinical neuroimaging perspective, providing a detailed overview of each step with practical advice. It discusses the application of handcrafted and deep radiomics in neuroimaging, stratified by neurological diagnosis. Although radiomics shows great potential for increasing diagnostic precision and improving treatment quality in neurology, several limitations hinder its clinical implementation. Addressing these challenges requires collaborative efforts, advancements in image harmonization methods, and the establishment of reproducible and standardized pipelines with transparent reporting. By overcoming these obstacles, radiomics can significantly impact clinical neurology and enhance patient care.

An anisotropy preserving metric for DTI processing

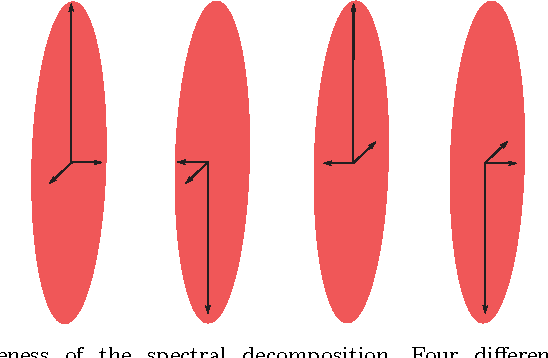
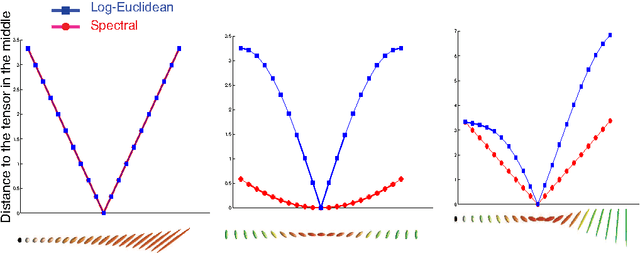
Statistical analysis of Diffusion Tensor Imaging (DTI) data requires a computational framework that is both numerically tractable (to account for the high dimensional nature of the data) and geometric (to account for the nonlinear nature of diffusion tensors). Building upon earlier studies that have shown that a Riemannian framework is appropriate to address these challenges, the present paper proposes a novel metric and an accompanying computational framework for DTI data processing. The proposed metric retains the geometry and the computational tractability of earlier methods grounded in the affine invariant metric. In addition, and in contrast to earlier methods, it provides an interpolation method which preserves anisotropy, a central information carried by diffusion tensor data.