Christoffel Doorman
Dynamic Network Reconfiguration for Entropy Maximization using Deep Reinforcement Learning
May 26, 2022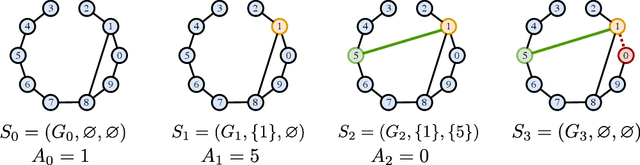
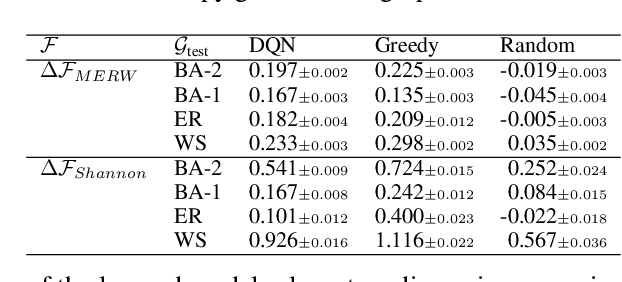


Abstract:A key problem in network theory is how to reconfigure a graph in order to optimize a quantifiable objective. Given the ubiquity of networked systems, such work has broad practical applications in a variety of situations, ranging from drug and material design to telecommunications. The large decision space of possible reconfigurations, however, makes this problem computationally intensive. In this paper, we cast the problem of network rewiring for optimizing a specified structural property as a Markov Decision Process (MDP), in which a decision-maker is given a budget of modifications that are performed sequentially. We then propose a general approach based on the Deep Q-Network (DQN) algorithm and graph neural networks (GNNs) that can efficiently learn strategies for rewiring networks. We then discuss a cybersecurity case study, i.e., an application to the computer network reconfiguration problem for intrusion protection. In a typical scenario, an attacker might have a (partial) map of the system they plan to penetrate; if the network is effectively "scrambled", they would not be able to navigate it since their prior knowledge would become obsolete. This can be viewed as an entropy maximization problem, in which the goal is to increase the surprise of the network. Indeed, entropy acts as a proxy measurement of the difficulty of navigating the network topology. We demonstrate the general ability of the proposed method to obtain better entropy gains than random rewiring on synthetic and real-world graphs while being computationally inexpensive, as well as being able to generalize to larger graphs than those seen during training. Simulations of attack scenarios confirm the effectiveness of the learned rewiring strategies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge