Disincentivizing Polarization in Social Networks

On social networks, algorithmic personalization drives users into filter bubbles where they rarely see content that deviates from their interests. We present a model for content curation and personalization that avoids filter bubbles, along with algorithmic guarantees and nearly matching lower bounds. In our model, the platform interacts with $n$ users over $T$ timesteps, choosing content for each user from $k$ categories. The platform receives stochastic rewards as in a multi-arm bandit. To avoid filter bubbles, we draw on the intuition that if some users are shown some category of content, then all users should see at least a small amount of that content. We first analyze a naive formalization of this intuition and show it has unintended consequences: it leads to ``tyranny of the majority'' with the burden of diversification borne disproportionately by those with minority interests. This leads us to our model which distributes this burden more equitably. We require that the probability any user is shown a particular type of content is at least $\gamma$ times the average probability all users are shown that type of content. Full personalization corresponds to $\gamma = 0$ and complete homogenization corresponds to $\gamma = 1$; hence, $\gamma$ encodes a hard cap on the level of personalization. We also analyze additional formulations where the platform can exceed its cap but pays a penalty proportional to its constraint violation. We provide algorithmic guarantees for optimizing recommendations subject to these constraints. These include nearly matching upper and lower bounds for the entire range of $\gamma \in [0,1]$ showing that the reward of a multi-agent variant of UCB is nearly optimal. Using real-world preference data, we empirically verify that under our model, users share the burden of diversification with only minor utility loss under our constraints.

An Algorithmic Introduction to Savings Circles

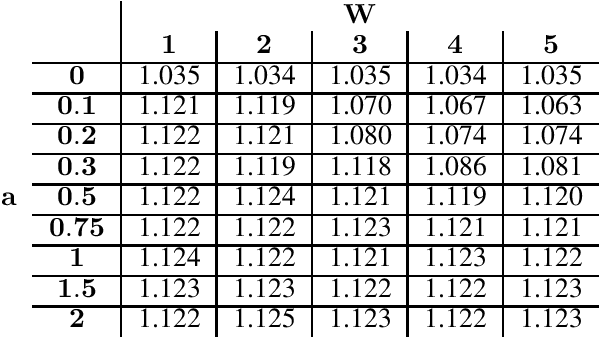
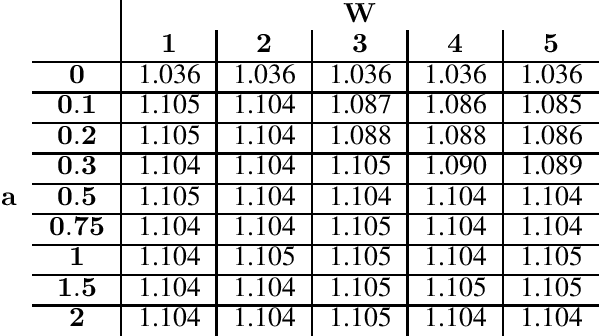
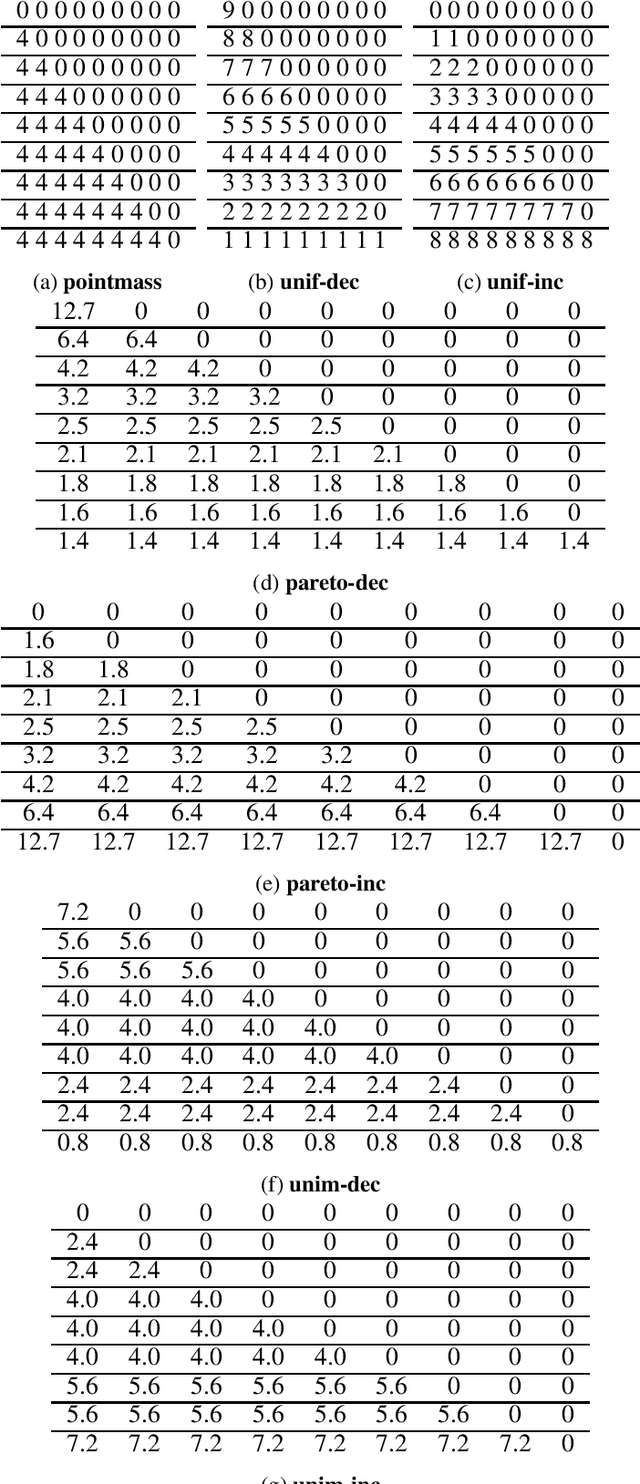
Rotating savings and credit associations (roscas) are informal financial organizations common in settings where communities have reduced access to formal financial institutions. In a rosca, a fixed group of participants regularly contribute sums of money to a pot. This pot is then allocated periodically using lottery, aftermarket, or auction mechanisms. Roscas are empirically well-studied in economics. They are, however, challenging to study theoretically due to their dynamic nature. Typical economic analyses of roscas stop at coarse ordinal welfare comparisons to other credit allocation mechanisms, leaving much of roscas' ubiquity unexplained. In this work, we take an algorithmic perspective on the study of roscas. Building on techniques from the price of anarchy literature, we present worst-case welfare approximation guarantees. We further experimentally compare the welfare of outcomes as key features of the environment vary. These cardinal welfare analyses further rationalize the prevalence of roscas. We conclude by discussing several other promising avenues.