Parameter Tuning of the Firefly Algorithm by Standard Monte Carlo and Quasi-Monte Carlo Methods

Almost all optimization algorithms have algorithm-dependent parameters, and the setting of such parameter values can significantly influence the behavior of the algorithm under consideration. Thus, proper parameter tuning should be carried out to ensure that the algorithm used for optimization performs well and is sufficiently robust for solving different types of optimization problems. In this study, the Firefly Algorithm (FA) is used to evaluate the influence of its parameter values on its efficiency. Parameter values are randomly initialized using both the standard Monte Carlo method and the Quasi Monte-Carlo method. The values are then used for tuning the FA. Two benchmark functions and a spring design problem are used to test the robustness of the tuned FA. From the preliminary findings, it can be deduced that both the Monte Carlo method and Quasi-Monte Carlo method produce similar results in terms of optimal fitness values. Numerical experiments using the two different methods on both benchmark functions and the spring design problem showed no major variations in the final fitness values, irrespective of the different sample values selected during the simulations. This insensitivity indicates the robustness of the FA.

Review of Parameter Tuning Methods for Nature-Inspired Algorithms

Almost all optimization algorithms have algorithm-dependent parameters, and the setting of such parameter values can largely influence the behaviour of the algorithm under consideration. Thus, proper parameter tuning should be carried out to ensure the algorithm used for optimization may perform well and can be sufficiently robust for solving different types of optimization problems. This chapter reviews some of the main methods for parameter tuning and then highlights the important issues concerning the latest development in parameter tuning. A few open problems are also discussed with some recommendations for future research.

True Global Optimality of the Pressure Vessel Design Problem: A Benchmark for Bio-Inspired Optimisation Algorithms

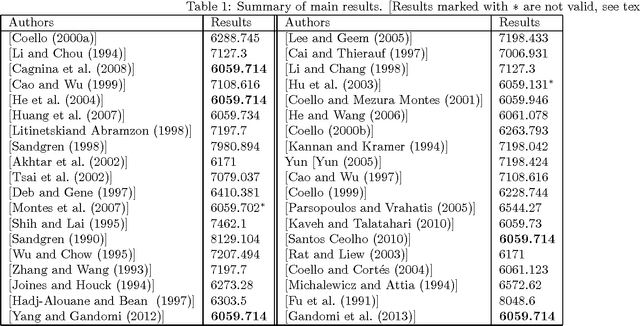
The pressure vessel design problem is a well-known design benchmark for validating bio-inspired optimization algorithms. However, its global optimality is not clear and there has been no mathematical proof put forward. In this paper, a detailed mathematical analysis of this problem is provided that proves that 6059.714335048436 is the global minimum. The Lagrange multiplier method is also used as an alternative proof and this method is extended to find the global optimum of a cantilever beam design problem.