Lower Bounds on the Depth of Integral ReLU Neural Networks via Lattice Polytopes

We prove that the set of functions representable by ReLU neural networks with integer weights strictly increases with the network depth while allowing arbitrary width. More precisely, we show that $\lceil\log_2(n)\rceil$ hidden layers are indeed necessary to compute the maximum of $n$ numbers, matching known upper bounds. Our results are based on the known duality between neural networks and Newton polytopes via tropical geometry. The integrality assumption implies that these Newton polytopes are lattice polytopes. Then, our depth lower bounds follow from a parity argument on the normalized volume of faces of such polytopes.

SCoT: Sense Clustering over Time: a tool for the analysis of lexical change

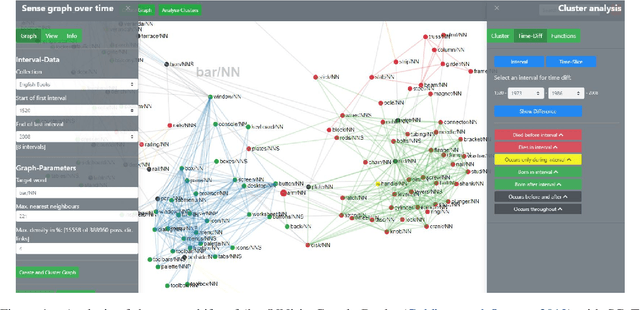
We present Sense Clustering over Time (SCoT), a novel network-based tool for analysing lexical change. SCoT represents the meanings of a word as clusters of similar words. It visualises their formation, change, and demise. There are two main approaches to the exploration of dynamic networks: the discrete one compares a series of clustered graphs from separate points in time. The continuous one analyses the changes of one dynamic network over a time-span. SCoT offers a new hybrid solution. First, it aggregates time-stamped documents into intervals and calculates one sense graph per discrete interval. Then, it merges the static graphs to a new type of dynamic semantic neighbourhood graph over time. The resulting sense clusters offer uniquely detailed insights into lexical change over continuous intervals with model transparency and provenance. SCoT has been successfully used in a European study on the changing meaning of `crisis'.