A Complete Parameterized Complexity Analysis of Bounded Planning

The propositional planning problem is a notoriously difficult computational problem, which remains hard even under strong syntactical and structural restrictions. Given its difficulty it becomes natural to study planning in the context of parameterized complexity. In this paper we continue the work initiated by Downey, Fellows and Stege on the parameterized complexity of planning with respect to the parameter "length of the solution plan." We provide a complete classification of the parameterized complexity of the planning problem under two of the most prominent syntactical restrictions, i.e., the so called PUBS restrictions introduced by Baeckstroem and Nebel and restrictions on the number of preconditions and effects as introduced by Bylander. We also determine which of the considered fixed-parameter tractable problems admit a polynomial kernel and which don't.

The Complexity of Planning Revisited - A Parameterized Analysis

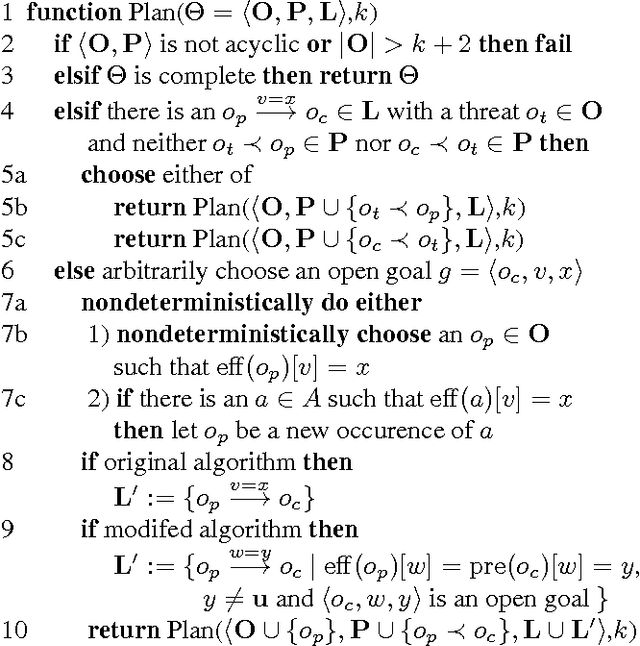
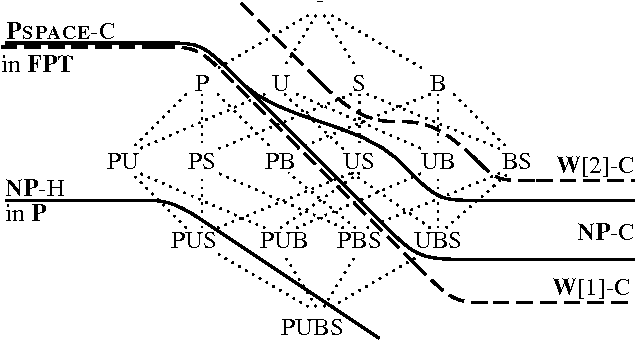
The early classifications of the computational complexity of planning under various restrictions in STRIPS (Bylander) and SAS+ (Baeckstroem and Nebel) have influenced following research in planning in many ways. We go back and reanalyse their subclasses, but this time using the more modern tool of parameterized complexity analysis. This provides new results that together with the old results give a more detailed picture of the complexity landscape. We demonstrate separation results not possible with standard complexity theory, which contributes to explaining why certain cases of planning have seemed simpler in practice than theory has predicted. In particular, we show that certain restrictions of practical interest are tractable in the parameterized sense of the term, and that a simple heuristic is sufficient to make a well-known partial-order planner exploit this fact.