A Refined View of Causal Graphs and Component Sizes: SP-Closed Graph Classes and Beyond

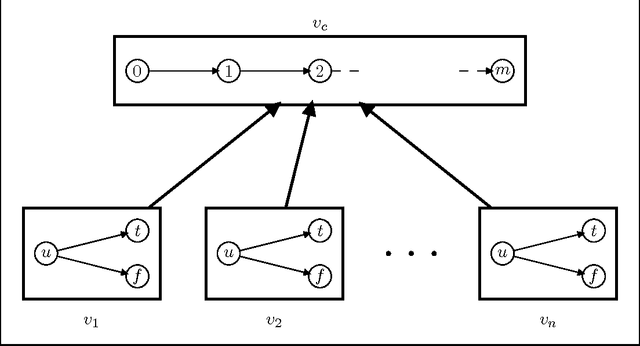
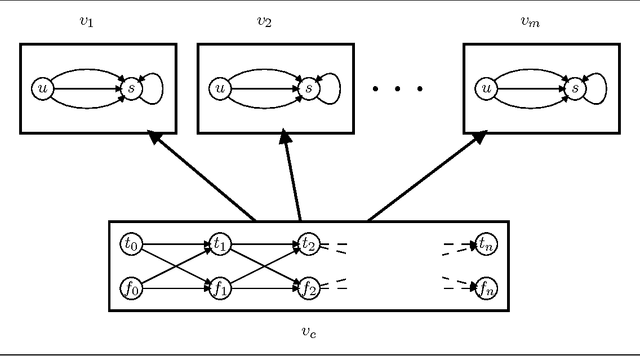
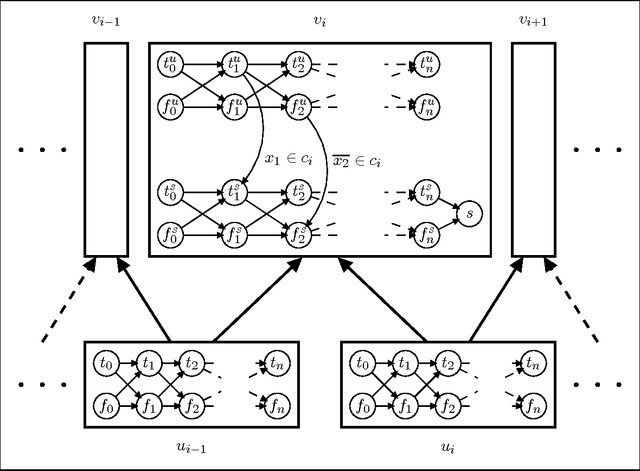
The causal graph of a planning instance is an important tool for planning both in practice and in theory. The theoretical studies of causal graphs have largely analysed the computational complexity of planning for instances where the causal graph has a certain structure, often in combination with other parameters like the domain size of the variables. Chen and Gimand#233;nez ignored even the structure and considered only the size of the weakly connected components. They proved that planning is tractable if the components are bounded by a constant and otherwise intractable. Their intractability result was, however, conditioned by an assumption from parameterised complexity theory that has no known useful relationship with the standard complexity classes. We approach the same problem from the perspective of standard complexity classes, and prove that planning is NP-hard for classes with unbounded components under an additional restriction we refer to as SP-closed. We then argue that most NP-hardness theorems for causal graphs are difficult to apply and, thus, prove a more general result; even if the component sizes grow slowly and the class is not densely populated with graphs, planning still cannot be tractable unless the polynomial hierachy collapses. Both these results still hold when restricted to the class of acyclic causal graphs. We finally give a partial characterization of the borderline between NP-hard and NP-intermediate classes, giving further insight into the problem.

Algorithms and Limits for Compact Plan Representations

Compact representations of objects is a common concept in computer science. Automated planning can be viewed as a case of this concept: a planning instance is a compact implicit representation of a graph and the problem is to find a path (a plan) in this graph. While the graphs themselves are represented compactly as planning instances, the paths are usually represented explicitly as sequences of actions. Some cases are known where the plans always have compact representations, for example, using macros. We show that these results do not extend to the general case, by proving a number of bounds for compact representations of plans under various criteria, like efficient sequential or random access of actions. In addition to this, we show that our results have consequences for what can be gained from reformulating planning into some other problem. As a contrast to this we also prove a number of positive results, demonstrating restricted cases where plans do have useful compact representations, as well as proving that macro plans have favourable access properties. Our results are finally discussed in relation to other relevant contexts.

Parameterized Complexity and Kernel Bounds for Hard Planning Problems

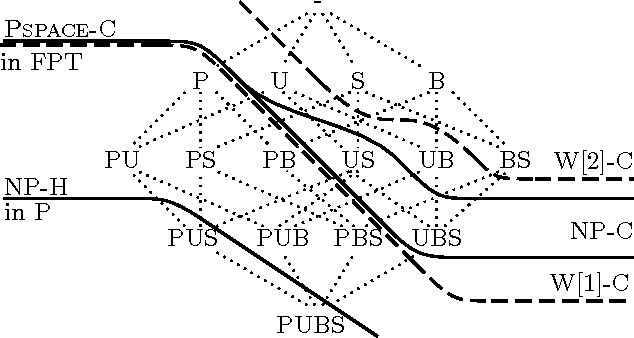
The propositional planning problem is a notoriously difficult computational problem. Downey et al. (1999) initiated the parameterized analysis of planning (with plan length as the parameter) and B\"ackstr\"om et al. (2012) picked up this line of research and provided an extensive parameterized analysis under various restrictions, leaving open only one stubborn case. We continue this work and provide a full classification. In particular, we show that the case when actions have no preconditions and at most $e$ postconditions is fixed-parameter tractable if $e\leq 2$ and W[1]-complete otherwise. We show fixed-parameter tractability by a reduction to a variant of the Steiner Tree problem; this problem has been shown fixed-parameter tractable by Guo et al. (2007). If a problem is fixed-parameter tractable, then it admits a polynomial-time self-reduction to instances whose input size is bounded by a function of the parameter, called the kernel. For some problems, this function is even polynomial which has desirable computational implications. Recent research in parameterized complexity has focused on classifying fixed-parameter tractable problems on whether they admit polynomial kernels or not. We revisit all the previously obtained restrictions of planning that are fixed-parameter tractable and show that none of them admits a polynomial kernel unless the polynomial hierarchy collapses to its third level.