SpecSphere: Dual-Pass Spectral-Spatial Graph Neural Networks with Certified Robustness

We introduce SpecSphere, the first dual-pass spectral-spatial GNN that certifies every prediction against both $\ell\_{0}$ edge flips and $\ell\_{\infty}$ feature perturbations, adapts to the full homophily-heterophily spectrum, and surpasses the expressive power of 1-Weisfeiler-Lehman while retaining linear-time complexity. Our model couples a Chebyshev-polynomial spectral branch with an attention-gated spatial branch and fuses their representations through a lightweight MLP trained in a cooperative-adversarial min-max game. We further establish (i) a uniform Chebyshev approximation theorem, (ii) minimax-optimal risk across the homophily-heterophily spectrum, (iii) closed-form robustness certificates, and (iv) universal approximation strictly beyond 1-WL. SpecSphere achieves state-of-the-art node-classification accuracy and delivers tighter certified robustness guarantees on real-world benchmarks. These results demonstrate that high expressivity, heterophily adaptation, and provable robustness can coexist within a single, scalable architecture.

Hierarchical Uncertainty-Aware Graph Neural Network

Recent research on graph neural networks (GNNs) has explored mechanisms for capturing local uncertainty and exploiting graph hierarchies to mitigate data sparsity and leverage structural properties. However, the synergistic integration of these two approaches remains underexplored. In this work, we introduce a novel architecture, the Hierarchical Uncertainty-Aware Graph Neural Network (HU-GNN), which unifies multi-scale representation learning, principled uncertainty estimation, and self-supervised embedding diversity within a single end-to-end framework. Specifically, HU-GNN adaptively forms node clusters and estimates uncertainty at multiple structural scales from individual nodes to higher levels. These uncertainty estimates guide a robust message-passing mechanism and attention weighting, effectively mitigating noise and adversarial perturbations while preserving predictive accuracy on both node- and graph-level tasks. We also offer key theoretical contributions, including a probabilistic formulation, rigorous uncertainty-calibration guarantees, and formal robustness bounds. Finally, by incorporating recent advances in graph contrastive learning, HU-GNN maintains diverse, structurally faithful embeddings. Extensive experiments on standard benchmarks demonstrate that our model achieves state-of-the-art robustness and interpretability.

Better Not to Propagate: Understanding Edge Uncertainty and Over-smoothing in Signed Graph Neural Networks

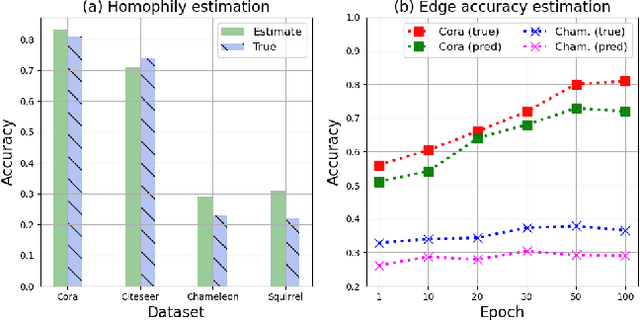
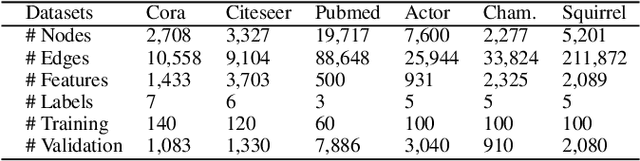
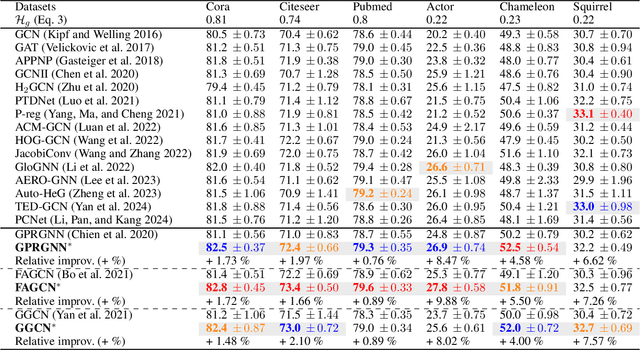
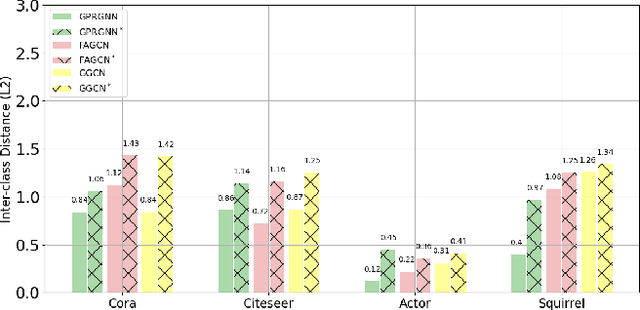
Traditional Graph Neural Networks (GNNs) rely on network homophily, which can lead to performance degradation due to over-smoothing in many real-world heterophily scenarios. Recent studies analyze the smoothing effect (separability) after message-passing (MP), depending on the expectation of node features. Regarding separability gain, they provided theoretical backgrounds on over-smoothing caused by various propagation schemes, including positive, signed, and blocked MPs. More recently, by extending these theorems, some works have suggested improvements in signed propagation under multiple classes. However, prior works assume that the error ratio of all propagation schemes is fixed, failing to investigate this phenomenon correctly. To solve this problem, we propose a novel method for estimating homophily and edge error ratio, integrated with dynamic selection between blocked and signed propagation during training. Our theoretical analysis, supported by extensive experiments, demonstrates that blocking MP can be more effective than signed propagation under high edge error ratios, improving the performance in both homophilic and heterophilic graphs.

Finding Heterophilic Neighbors via Confidence-based Subgraph Matching for Semi-supervised Node Classification

Graph Neural Networks (GNNs) have proven to be powerful in many graph-based applications. However, they fail to generalize well under heterophilic setups, where neighbor nodes have different labels. To address this challenge, we employ a confidence ratio as a hyper-parameter, assuming that some of the edges are disassortative (heterophilic). Here, we propose a two-phased algorithm. Firstly, we determine edge coefficients through subgraph matching using a supplementary module. Then, we apply GNNs with a modified label propagation mechanism to utilize the edge coefficients effectively. Specifically, our supplementary module identifies a certain proportion of task-irrelevant edges based on a given confidence ratio. Using the remaining edges, we employ the widely used optimal transport to measure the similarity between two nodes with their subgraphs. Finally, using the coefficients as supplementary information on GNNs, we improve the label propagation mechanism which can prevent two nodes with smaller weights from being closer. The experiments on benchmark datasets show that our model alleviates over-smoothing and improves performance.

Is Signed Message Essential for Graph Neural Networks?

Message-passing Graph Neural Networks (GNNs), which collect information from adjacent nodes, achieve satisfying results on homophilic graphs. However, their performances are dismal in heterophilous graphs, and many researchers have proposed a plethora of schemes to solve this problem. Especially, flipping the sign of edges is rooted in a strong theoretical foundation, and attains significant performance enhancements. Nonetheless, previous analyses assume a binary class scenario and they may suffer from confined applicability. This paper extends the prior understandings to multi-class scenarios and points out two drawbacks: (1) the sign of multi-hop neighbors depends on the message propagation paths and may incur inconsistency, (2) it also increases the prediction uncertainty (e.g., conflict evidence) which can impede the stability of the algorithm. Based on the theoretical understanding, we introduce a novel strategy that is applicable to multi-class graphs. The proposed scheme combines confidence calibration to secure robustness while reducing uncertainty. We show the efficacy of our theorem through extensive experiments on six benchmark graph datasets.

Signed Directed Graph Contrastive Learning with Laplacian Augmentation

Graph contrastive learning has become a powerful technique for several graph mining tasks. It learns discriminative representation from different perspectives of augmented graphs. Ubiquitous in our daily life, singed-directed graphs are the most complex and tricky to analyze among various graph types. That is why singed-directed graph contrastive learning has not been studied much yet, while there are many contrastive studies for unsigned and undirected. Thus, this paper proposes a novel signed-directed graph contrastive learning, SDGCL. It makes two different structurally perturbed graph views and gets node representations via magnetic Laplacian perturbation. We use a node-level contrastive loss to maximize the mutual information between the two graph views. The model is jointly learned with contrastive and supervised objectives. The graph encoder of SDGCL does not depend on social theories or predefined assumptions. Therefore it does not require finding triads or selecting neighbors to aggregate. It leverages only the edge signs and directions via magnetic Laplacian. To the best of our knowledge, it is the first to introduce magnetic Laplacian perturbation and signed spectral graph contrastive learning. The superiority of the proposed model is demonstrated through exhaustive experiments on four real-world datasets. SDGCL shows better performance than other state-of-the-art on four evaluation metrics.

Flip Initial Features: Generalization of Neural Networks for Semi-supervised Node Classification

Graph neural networks (GNNs) have been widely used under semi-supervised settings. Prior studies have mainly focused on finding appropriate graph filters (e.g., aggregation schemes) to generalize well for both homophilic and heterophilic graphs. Even though these approaches are essential and effective, they still suffer from the sparsity in initial node features inherent in the bag-of-words representation. Common in semi-supervised learning where the training samples often fail to cover the entire dimensions of graph filters (hyperplanes), this can precipitate over-fitting of specific dimensions in the first projection matrix. To deal with this problem, we suggest a simple and novel strategy; create additional space by flipping the initial features and hyperplane simultaneously. Training in both the original and in the flip space can provide precise updates of learnable parameters. To the best of our knowledge, this is the first attempt that effectively moderates the overfitting problem in GNN. Extensive experiments on real-world datasets demonstrate that the proposed technique improves the node classification accuracy up to 40.2 %