Revisiting Design Choices in Proximal Policy Optimization

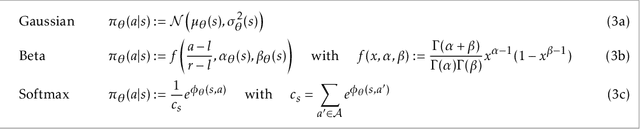
Proximal Policy Optimization (PPO) is a popular deep policy gradient algorithm. In standard implementations, PPO regularizes policy updates with clipped probability ratios, and parameterizes policies with either continuous Gaussian distributions or discrete Softmax distributions. These design choices are widely accepted, and motivated by empirical performance comparisons on MuJoCo and Atari benchmarks. We revisit these practices outside the regime of current benchmarks, and expose three failure modes of standard PPO. We explain why standard design choices are problematic in these cases, and show that alternative choices of surrogate objectives and policy parameterizations can prevent the failure modes. We hope that our work serves as a reminder that many algorithmic design choices in reinforcement learning are tied to specific simulation environments. We should not implicitly accept these choices as a standard part of a more general algorithm.

Linear Dynamics: Clustering without identification

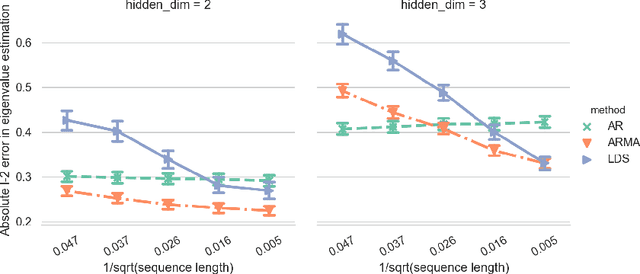
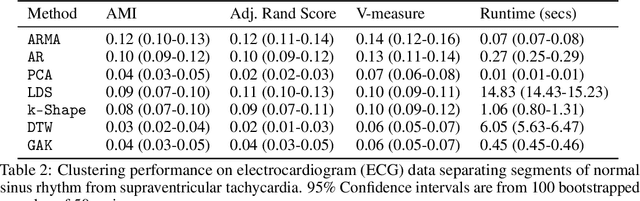
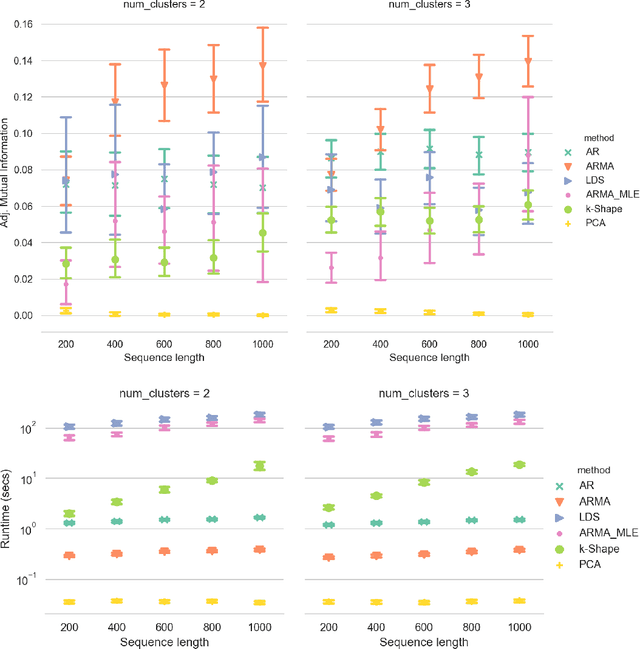
Clustering time series is a delicate task; varying lengths and temporal offsets obscure direct comparisons. A natural strategy is to learn a parametric model foreach time series and to cluster the model parameters rather than the sequences themselves. Linear dynamical systems are a fundamental and powerful parametric model class. However, identifying the parameters of a linear dynamical systems is a venerable task, permitting provably efficient solutions only in special cases. In this work, we show that clustering the parameters of unknown linear dynamical systems is, in fact, easier than identifying them. We analyze a computationally efficient clustering algorithm that enjoys provable convergence guarantees under a natural separation assumption. Although easy to implement, our algorithm is general, handling multi-dimensional data with time offsets and partial sequences. Evaluating our algorithm on both synthetic data and real electrocardiogram (ECG) signals, we see significant improvements in clustering quality over existing baselines.