Linear Dynamics: Clustering without identification

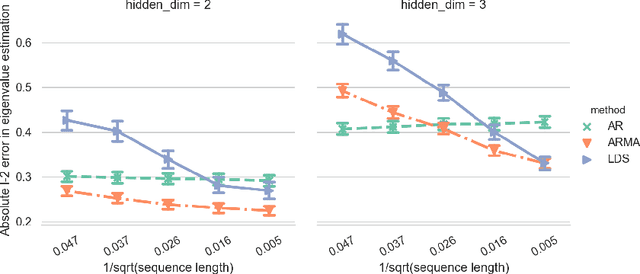
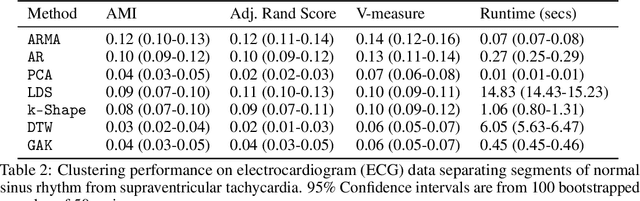
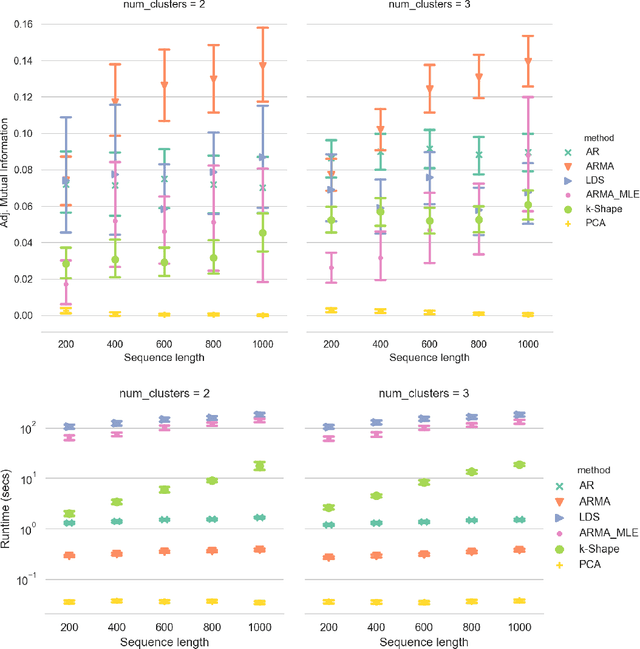
Clustering time series is a delicate task; varying lengths and temporal offsets obscure direct comparisons. A natural strategy is to learn a parametric model foreach time series and to cluster the model parameters rather than the sequences themselves. Linear dynamical systems are a fundamental and powerful parametric model class. However, identifying the parameters of a linear dynamical systems is a venerable task, permitting provably efficient solutions only in special cases. In this work, we show that clustering the parameters of unknown linear dynamical systems is, in fact, easier than identifying them. We analyze a computationally efficient clustering algorithm that enjoys provable convergence guarantees under a natural separation assumption. Although easy to implement, our algorithm is general, handling multi-dimensional data with time offsets and partial sequences. Evaluating our algorithm on both synthetic data and real electrocardiogram (ECG) signals, we see significant improvements in clustering quality over existing baselines.