A new locally linear embedding scheme in light of Hessian eigenmap

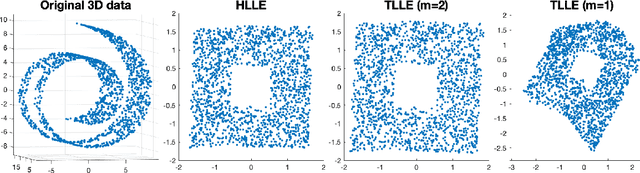
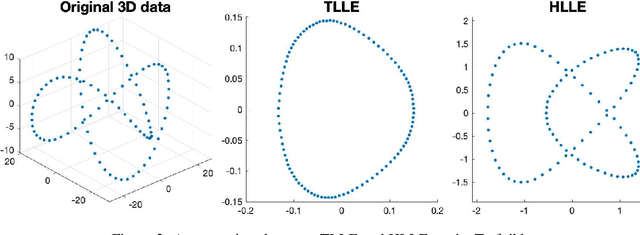
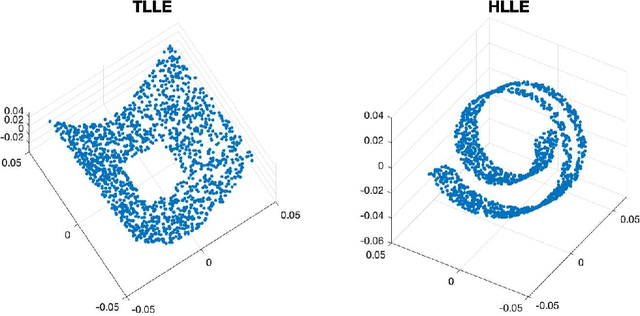
We provide a new interpretation of Hessian locally linear embedding (HLLE), revealing that it is essentially a variant way to implement the same idea of locally linear embedding (LLE). Based on the new interpretation, a substantial simplification can be made, in which the idea of "Hessian" is replaced by rather arbitrary weights. Moreover, we show by numerical examples that HLLE may produce projection-like results when the dimension of the target space is larger than that of the data manifold, and hence one further modification concerning the manifold dimension is suggested. Combining all the observations, we finally achieve a new LLE-type method, which is called tangential LLE (TLLE). It is simpler and more robust than HLLE.

The Unsupervised Method of Vessel Movement Trajectory Prediction

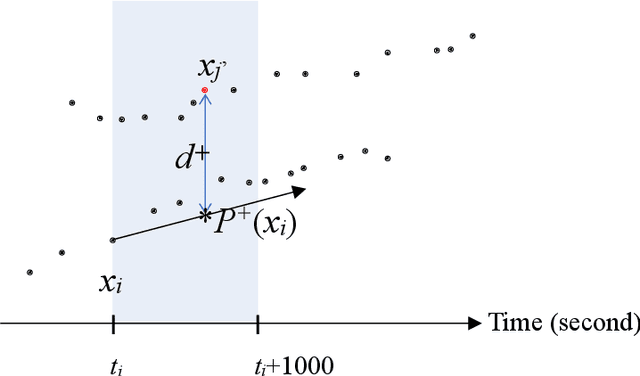
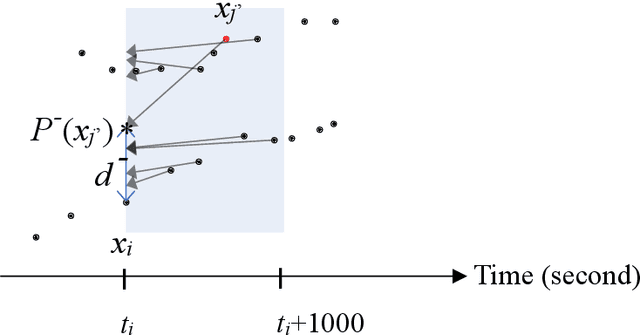
In real-world application scenarios, it is crucial for marine navigators and security analysts to predict vessel movement trajectories at sea based on the Automated Identification System (AIS) data in a given time span. This article presents an unsupervised method of ship movement trajectory prediction which represents the data in a three-dimensional space which consists of time difference between points, the scaled error distance between the tested and its predicted forward and backward locations, and the space-time angle. The representation feature space reduces the search scope for the next point to a collection of candidates which fit the local path prediction well, and therefore improve the accuracy. Unlike most statistical learning or deep learning methods, the proposed clustering-based trajectory reconstruction method does not require computationally expensive model training. This makes real-time reliable and accurate prediction feasible without using a training set. Our results show that the most prediction trajectories accurately consist of the true vessel paths.