A new locally linear embedding scheme in light of Hessian eigenmap
Paper and Code
Dec 16, 2021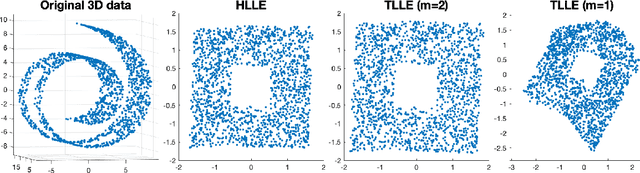
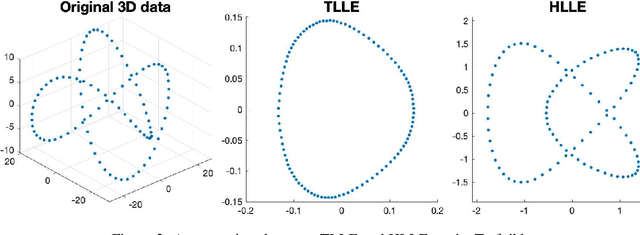
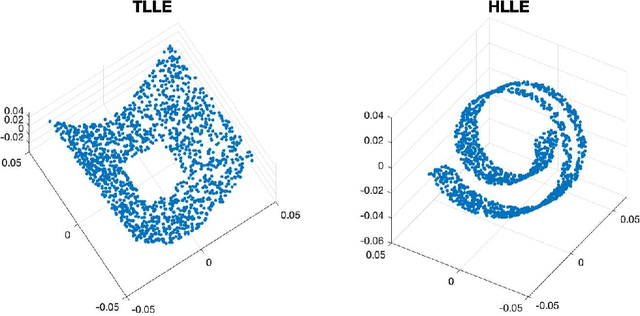
We provide a new interpretation of Hessian locally linear embedding (HLLE), revealing that it is essentially a variant way to implement the same idea of locally linear embedding (LLE). Based on the new interpretation, a substantial simplification can be made, in which the idea of "Hessian" is replaced by rather arbitrary weights. Moreover, we show by numerical examples that HLLE may produce projection-like results when the dimension of the target space is larger than that of the data manifold, and hence one further modification concerning the manifold dimension is suggested. Combining all the observations, we finally achieve a new LLE-type method, which is called tangential LLE (TLLE). It is simpler and more robust than HLLE.
* 13 pages
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge