Unsupervised Learning of Initialization in Deep Neural Networks via Maximum Mean Discrepancy

Despite the recent success of stochastic gradient descent in deep learning, it is often difficult to train a deep neural network with an inappropriate choice of its initial parameters. Even if training is successful, it has been known that the initial parameter configuration may negatively impact generalization. In this paper, we propose an unsupervised algorithm to find good initialization for input data, given that a downstream task is d-way classification. We first notice that each parameter configuration in the parameter space corresponds to one particular downstream task of d-way classification. We then conjecture that the success of learning is directly related to how diverse downstream tasks are in the vicinity of the initial parameters. We thus design an algorithm that encourages small perturbation to the initial parameter configuration leads to a diverse set of d-way classification tasks. In other words, the proposed algorithm ensures a solution to any downstream task to be near the initial parameter configuration. We empirically evaluate the proposed algorithm on various tasks derived from MNIST with a fully connected network. In these experiments, we observe that our algorithm improves average test accuracy across most of these tasks, and that such improvement is greater when the number of labelled examples is small.

A Non-monotonic Self-terminating Language Model

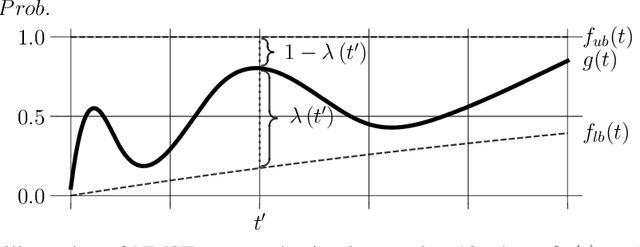
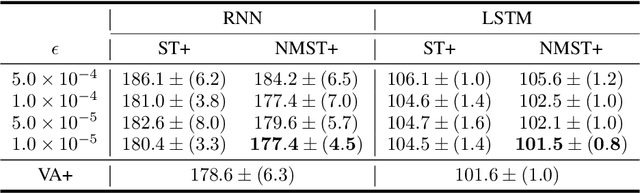
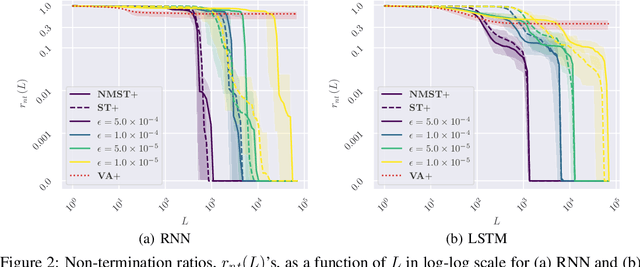
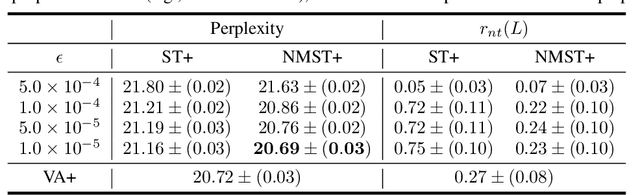
Recent large-scale neural autoregressive sequence models have shown impressive performances on a variety of natural language generation tasks. However, their generated sequences often exhibit degenerate properties such as non-termination, undesirable repetition, and premature termination, when generated with decoding algorithms such as greedy search, beam search, top-$k$ sampling, and nucleus sampling. In this paper, we focus on the problem of non-terminating sequences resulting from an incomplete decoding algorithm. We first define an incomplete probable decoding algorithm which includes greedy search, top-$k$ sampling, and nucleus sampling, beyond the incomplete decoding algorithm originally put forward by Welleck et al. (2020). We then propose a non-monotonic self-terminating language model, which significantly relaxes the constraint of monotonically increasing termination probability in the originally proposed self-terminating language model by Welleck et al. (2020), to address the issue of non-terminating sequences when using incomplete probable decoding algorithms. We prove that our proposed model prevents non-terminating sequences when using not only incomplete probable decoding algorithms but also beam search. We empirically validate our model on sequence completion tasks with various architectures.

Mixout: Effective Regularization to Finetune Large-scale Pretrained Language Models

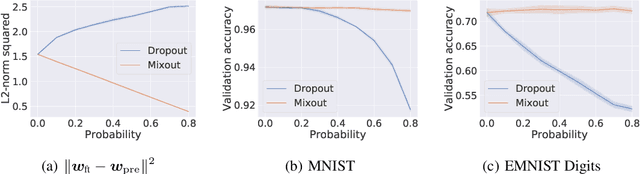
In natural language processing, it has been observed recently that generalization could be greatly improved by finetuning a large-scale language model pretrained on a large unlabeled corpus. Despite its recent success and wide adoption, finetuning a large pretrained language model on a downstream task is prone to degenerate performance when there are only a small number of training instances available. In this paper, we introduce a new regularization technique, to which we refer as "mixout", motivated by dropout. Mixout stochastically mixes the parameters of two models. We show that our mixout technique regularizes learning to minimize the deviation from one of the two models and that the strength of regularization adapts along the optimization trajectory. We empirically evaluate the proposed mixout and its variants on finetuning a pretrained language model on downstream tasks. More specifically, we demonstrate that the stability of finetuning and the average accuracy greatly increase when we use the proposed approach to regularize finetuning of BERT on downstream tasks in GLUE.

Directional Analysis of Stochastic Gradient Descent via von Mises-Fisher Distributions in Deep learning

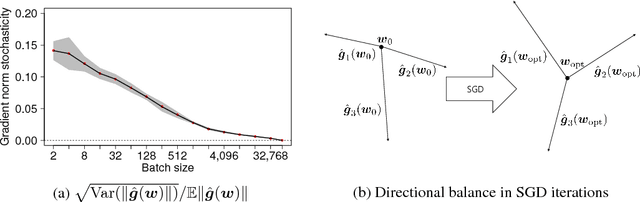
Although stochastic gradient descent (SGD) is a driving force behind the recent success of deep learning, our understanding of its dynamics in a high-dimensional parameter space is limited. In recent years, some researchers have used the stochasticity of minibatch gradients, or the signal-to-noise ratio, to better characterize the learning dynamics of SGD. Inspired from these work, we here analyze SGD from a geometrical perspective by inspecting the stochasticity of the norms and directions of minibatch gradients. We propose a model of the directional concentration for minibatch gradients through von Mises-Fisher (VMF) distribution, and show that the directional uniformity of minibatch gradients increases over the course of SGD. We empirically verify our result using deep convolutional networks and observe a higher correlation between the gradient stochasticity and the proposed directional uniformity than that against the gradient norm stochasticity, suggesting that the directional statistics of minibatch gradients is a major factor behind SGD.