Logistic Regression Augmented Community Detection for Network Data with Application in Identifying Autism-Related Gene Pathways

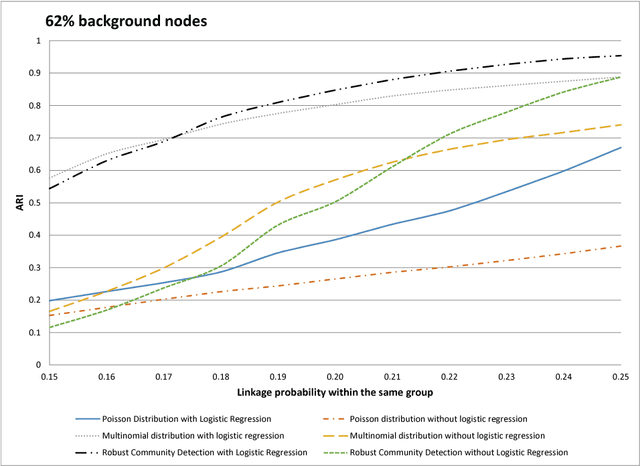
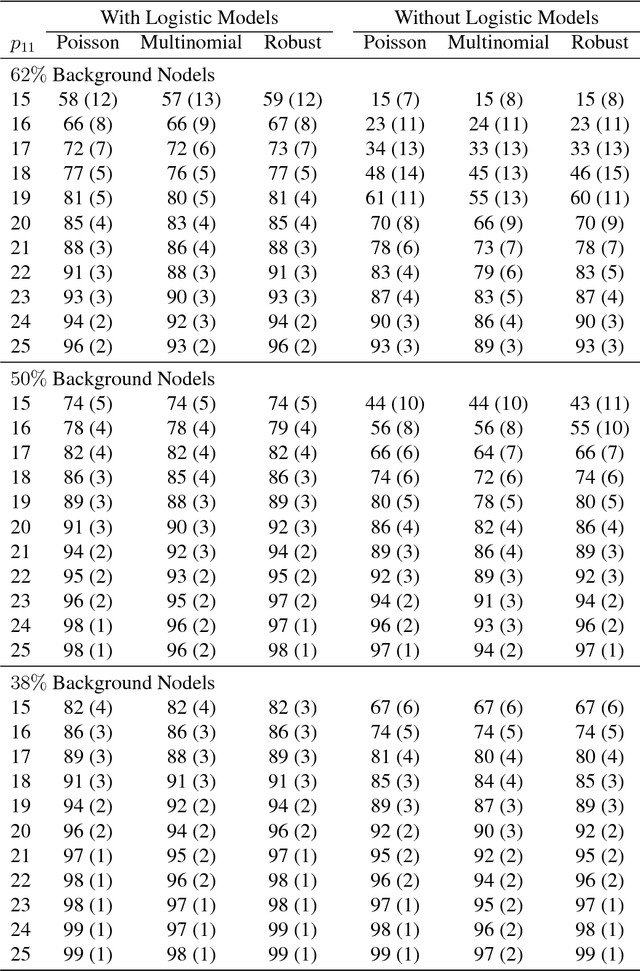
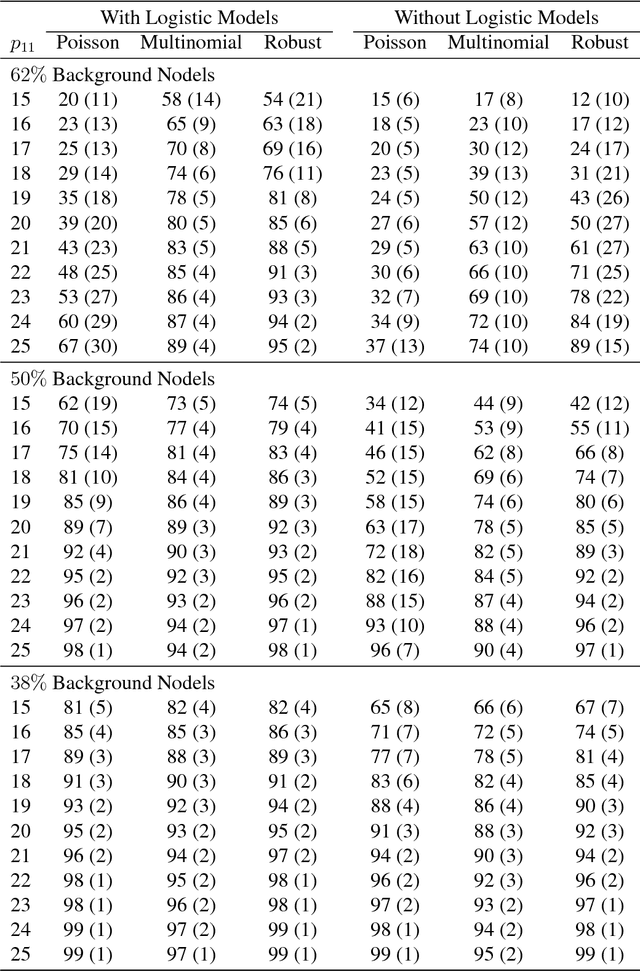
When searching for gene pathways leading to specific disease outcomes, additional information on gene characteristics is often available that may facilitate to differentiate genes related to the disease from irrelevant background when connections involving both types of genes are observed and their relationships to the disease are unknown. We propose method to single out irrelevant background genes with the help of auxiliary information through a logistic regression, and cluster relevant genes into cohesive groups using the adjacency matrix. Expectation-maximization algorithm is modified to maximize a joint pseudo-likelihood assuming latent indicators for relevance to the disease and latent group memberships as well as Poisson or multinomial distributed link numbers within and between groups. A robust version allowing arbitrary linkage patterns within the background is further derived. Asymptotic consistency of label assignments under the stochastic blockmodel is proven. Superior performance and robustness in finite samples are observed in simulation studies. The proposed robust method identifies previously missed gene sets underlying autism related neurological diseases using diverse data sources including de novo mutations, gene expressions and protein-protein interactions.

On Consistency of Graph-based Semi-supervised Learning

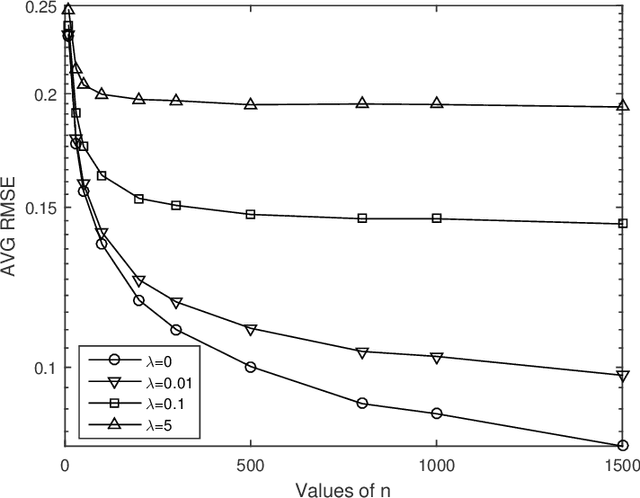
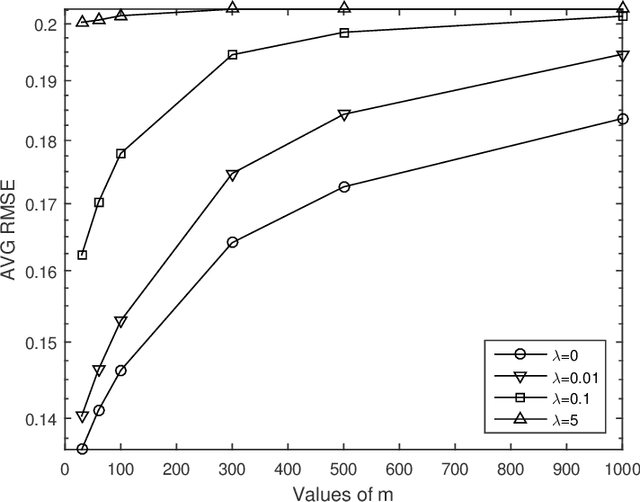
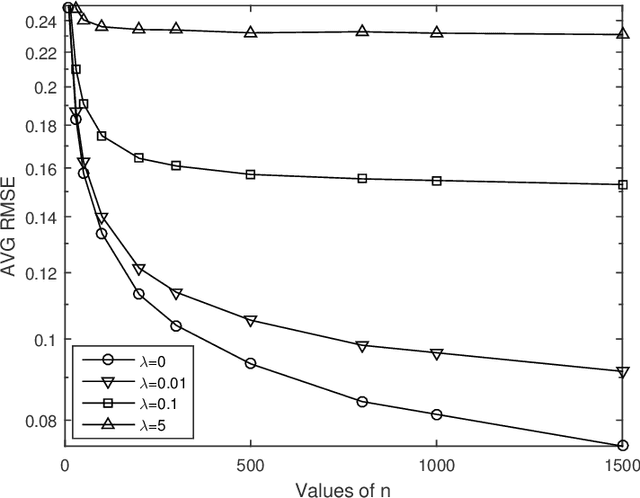
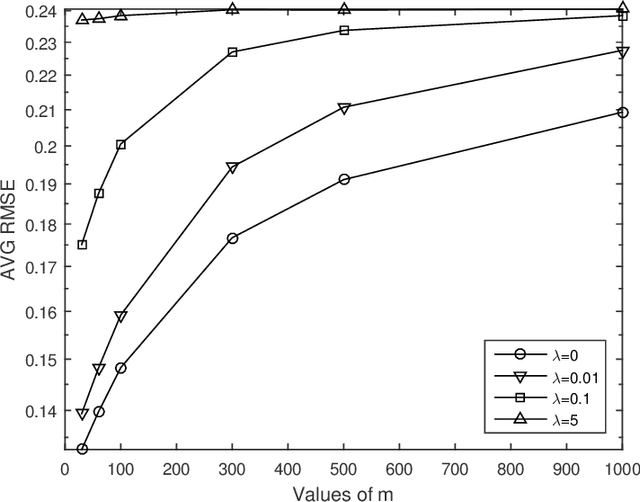
Graph-based semi-supervised learning is one of the most popular methods in machine learning. Some of its theoretical properties such as bounds for the generalization error and the convergence of the graph Laplacian regularizer have been studied in computer science and statistics literatures. However, a fundamental statistical property, the consistency of the estimator from this method has not been proved. In this article, we study the consistency problem under a non-parametric framework. We prove the consistency of graph-based learning in the case that the estimated scores are enforced to be equal to the observed responses for the labeled data. The sample sizes of both labeled and unlabeled data are allowed to grow in this result. When the estimated scores are not required to be equal to the observed responses, a tuning parameter is used to balance the loss function and the graph Laplacian regularizer. We give a counterexample demonstrating that the estimator for this case can be inconsistent. The theoretical findings are supported by numerical studies.