On Consistency of Graph-based Semi-supervised Learning
Paper and Code
Mar 17, 2017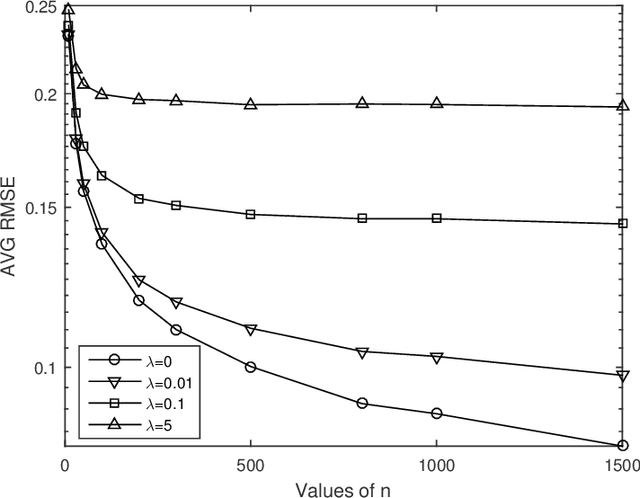
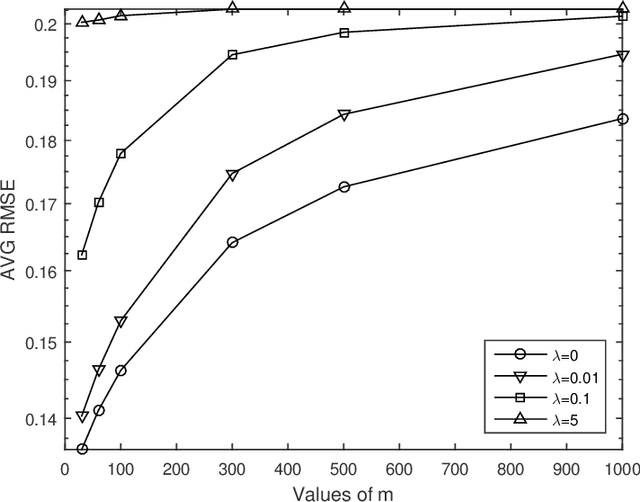
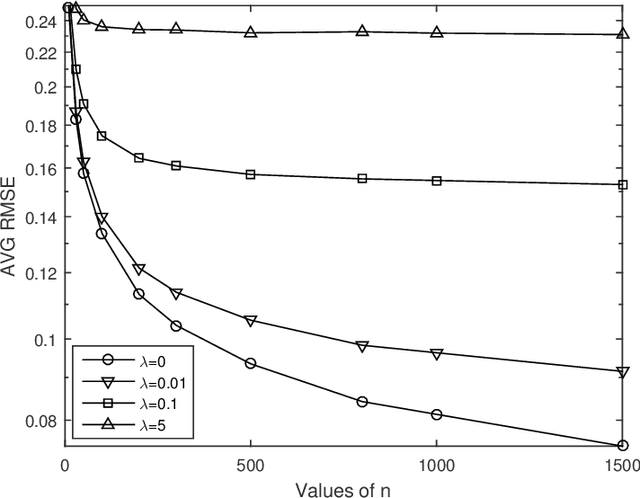
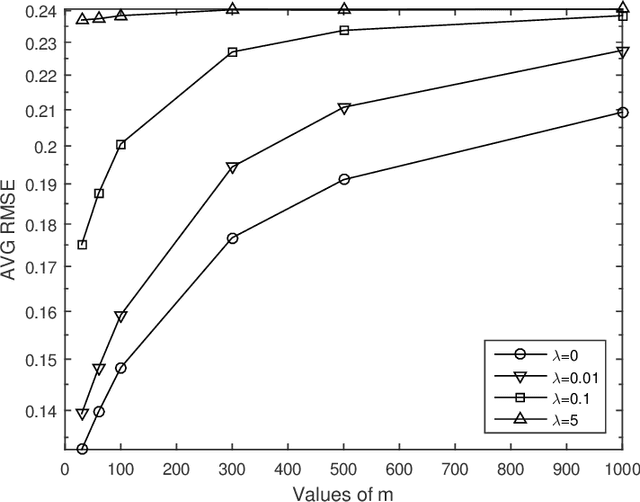
Graph-based semi-supervised learning is one of the most popular methods in machine learning. Some of its theoretical properties such as bounds for the generalization error and the convergence of the graph Laplacian regularizer have been studied in computer science and statistics literatures. However, a fundamental statistical property, the consistency of the estimator from this method has not been proved. In this article, we study the consistency problem under a non-parametric framework. We prove the consistency of graph-based learning in the case that the estimated scores are enforced to be equal to the observed responses for the labeled data. The sample sizes of both labeled and unlabeled data are allowed to grow in this result. When the estimated scores are not required to be equal to the observed responses, a tuning parameter is used to balance the loss function and the graph Laplacian regularizer. We give a counterexample demonstrating that the estimator for this case can be inconsistent. The theoretical findings are supported by numerical studies.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge