How Much Can Time-related Features Enhance Time Series Forecasting?

Recent advancements in long-term time series forecasting (LTSF) have primarily focused on capturing cross-time and cross-variate (channel) dependencies within historical data. However, a critical aspect often overlooked by many existing methods is the explicit incorporation of \textbf{time-related features} (e.g., season, month, day of the week, hour, minute), which are essential components of time series data. The absence of this explicit time-related encoding limits the ability of current models to capture cyclical or seasonal trends and long-term dependencies, especially with limited historical input. To address this gap, we introduce a simple yet highly efficient module designed to encode time-related features, Time Stamp Forecaster (TimeSter), thereby enhancing the backbone's forecasting performance. By integrating TimeSter with a linear backbone, our model, TimeLinear, significantly improves the performance of a single linear projector, reducing MSE by an average of 23\% on benchmark datasets such as Electricity and Traffic. Notably, TimeLinear achieves these gains while maintaining exceptional computational efficiency, delivering results that are on par with or exceed state-of-the-art models, despite using a fraction of the parameters.

C-Mamba: Channel Correlation Enhanced State Space Models for Multivariate Time Series Forecasting

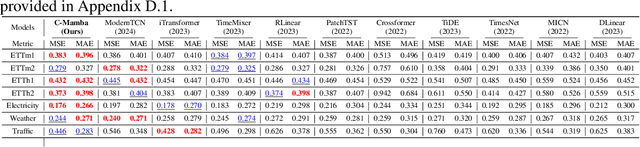
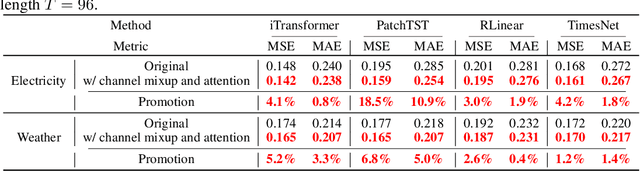
In recent years, significant progress has been made in multivariate time series forecasting using Linear-based, Transformer-based, and Convolution-based models. However, these approaches face notable limitations: linear forecasters struggle with representation capacities, attention mechanisms suffer from quadratic complexity, and convolutional models have a restricted receptive field. These constraints impede their effectiveness in modeling complex time series, particularly those with numerous variables. Additionally, many models adopt the Channel-Independent (CI) strategy, treating multivariate time series as uncorrelated univariate series while ignoring their correlations. For models considering inter-channel relationships, whether through the self-attention mechanism, linear combination, or convolution, they all incur high computational costs and focus solely on weighted summation relationships, neglecting potential proportional relationships between channels. In this work, we address these issues by leveraging the newly introduced state space model and propose \textbf{C-Mamba}, a novel approach that captures cross-channel dependencies while maintaining linear complexity without losing the global receptive field. Our model consists of two key components: (i) channel mixup, where two channels are mixed to enhance the training sets; (ii) channel attention enhanced patch-wise Mamba encoder that leverages the ability of the state space models to capture cross-time dependencies and models correlations between channels by mining their weight relationships. Our model achieves state-of-the-art performance on seven real-world time series datasets. Moreover, the proposed mixup and attention strategy exhibits strong generalizability across other frameworks.

Graph Data Condensation via Self-expressive Graph Structure Reconstruction

With the increasing demands of training graph neural networks (GNNs) on large-scale graphs, graph data condensation has emerged as a critical technique to relieve the storage and time costs during the training phase. It aims to condense the original large-scale graph to a much smaller synthetic graph while preserving the essential information necessary for efficiently training a downstream GNN. However, existing methods concentrate either on optimizing node features exclusively or endeavor to independently learn node features and the graph structure generator. They could not explicitly leverage the information of the original graph structure and failed to construct an interpretable graph structure for the synthetic dataset. To address these issues, we introduce a novel framework named \textbf{G}raph Data \textbf{C}ondensation via \textbf{S}elf-expressive Graph Structure \textbf{R}econstruction (\textbf{GCSR}). Our method stands out by (1) explicitly incorporating the original graph structure into the condensing process and (2) capturing the nuanced interdependencies between the condensed nodes by reconstructing an interpretable self-expressive graph structure. Extensive experiments and comprehensive analysis validate the efficacy of the proposed method across diverse GNN models and datasets. Our code is available at https://www.dropbox.com/scl/fi/2aonyp5ln5gisdqtjimu8/GCSR.zip?rlkey=11cuwfpsf54wxiiktu0klud0x&dl=0