Changhong Zhao
A Data-Driven Real-Time Optimal Power Flow Algorithm Using Local Feedback
Feb 21, 2025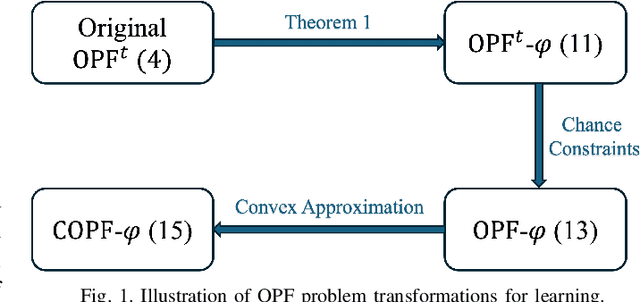
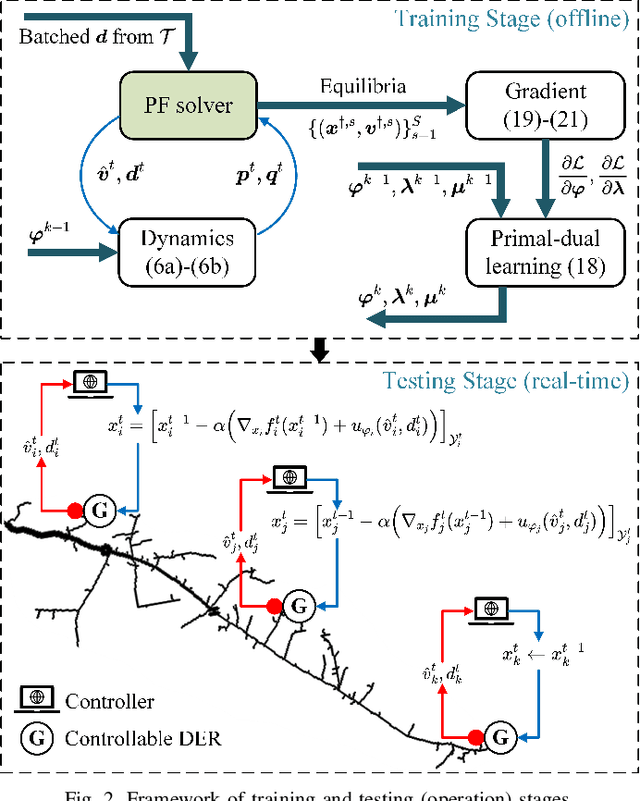
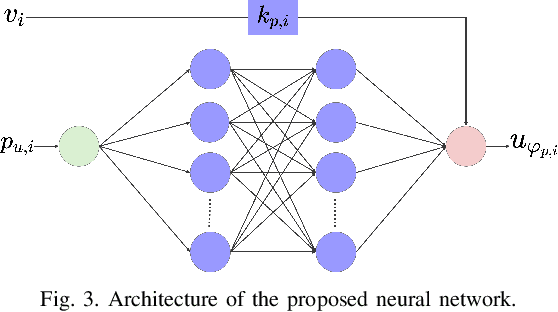
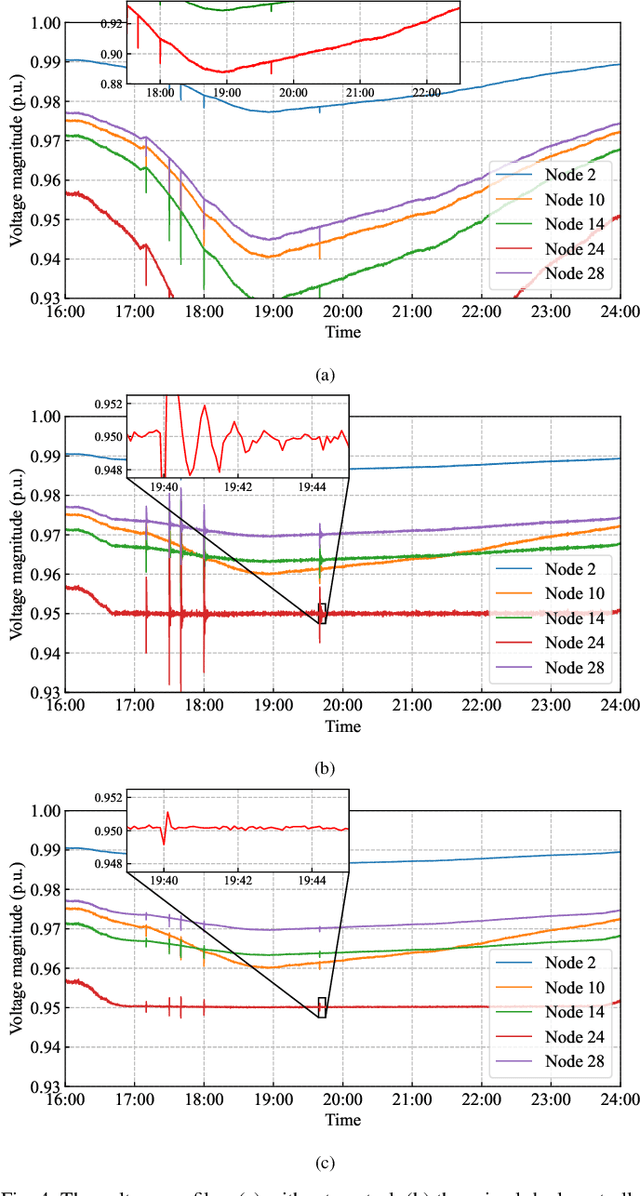
Abstract:The increasing penetration of distributed energy resources (DERs) adds variability as well as fast control capabilities to power networks. Dispatching the DERs based on local information to provide real-time optimal network operation is the desideratum. In this paper, we propose a data-driven real-time algorithm that uses only the local measurements to solve time-varying AC optimal power flow (OPF). Specifically, we design a learnable function that takes the local feedback as input in the algorithm. The learnable function, under certain conditions, will result in a unique stationary point of the algorithm, which in turn transfers the OPF problems to be optimized over the parameters of the function. We then develop a stochastic primal-dual update to solve the variant of the OPF problems based on a deep neural network (DNN) parametrization of the learnable function, which is referred to as the training stage. We also design a gradient-free alternative to bypass the cumbersome gradient calculation of the nonlinear power flow model. The OPF solution-tracking error bound is established in the sense of universal approximation of DNN. Numerical results on the IEEE 37-bus test feeder show that the proposed method can track the time-varying OPF solutions with higher accuracy and faster computation compared to benchmark methods.
DeepOPF-U: A Unified Deep Neural Network to Solve AC Optimal Power Flow in Multiple Networks
Sep 22, 2023
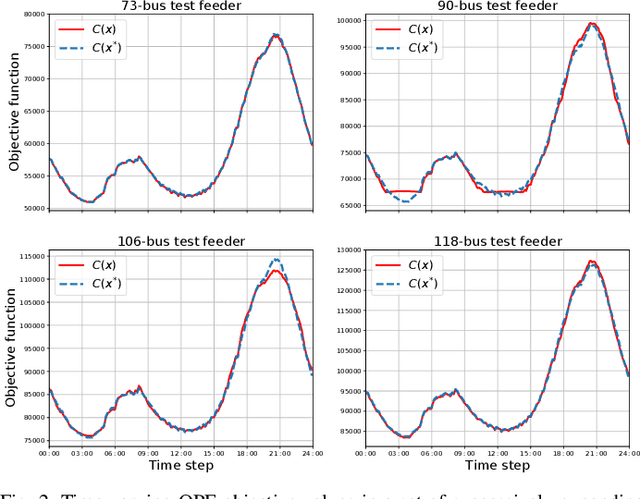


Abstract:The traditional machine learning models to solve optimal power flow (OPF) are mostly trained for a given power network and lack generalizability to today's power networks with varying topologies and growing plug-and-play distributed energy resources (DERs). In this paper, we propose DeepOPF-U, which uses one unified deep neural network (DNN) to solve alternating-current (AC) OPF problems in different power networks, including a set of power networks that is successively expanding. Specifically, we design elastic input and output layers for the vectors of given loads and OPF solutions with varying lengths in different networks. The proposed method, using a single unified DNN, can deal with different and growing numbers of buses, lines, loads, and DERs. Simulations of IEEE 57/118/300-bus test systems and a network growing from 73 to 118 buses verify the improved performance of DeepOPF-U compared to existing DNN-based solution methods.
Differentially Private Stochastic Convex Optimization in (Non)-Euclidean Space Revisited
Mar 31, 2023

Abstract:In this paper, we revisit the problem of Differentially Private Stochastic Convex Optimization (DP-SCO) in Euclidean and general $\ell_p^d$ spaces. Specifically, we focus on three settings that are still far from well understood: (1) DP-SCO over a constrained and bounded (convex) set in Euclidean space; (2) unconstrained DP-SCO in $\ell_p^d$ space; (3) DP-SCO with heavy-tailed data over a constrained and bounded set in $\ell_p^d$ space. For problem (1), for both convex and strongly convex loss functions, we propose methods whose outputs could achieve (expected) excess population risks that are only dependent on the Gaussian width of the constraint set rather than the dimension of the space. Moreover, we also show the bound for strongly convex functions is optimal up to a logarithmic factor. For problems (2) and (3), we propose several novel algorithms and provide the first theoretical results for both cases when $1<p<2$ and $2\leq p\leq \infty$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge