Dataset-Free Weight-Initialization on Restricted Boltzmann Machine

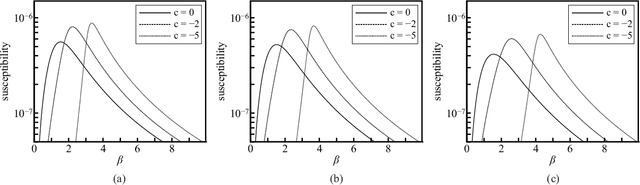
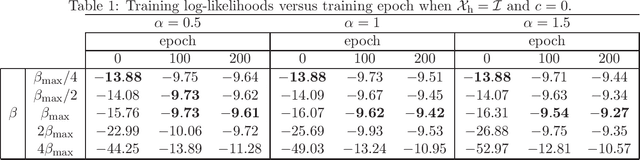
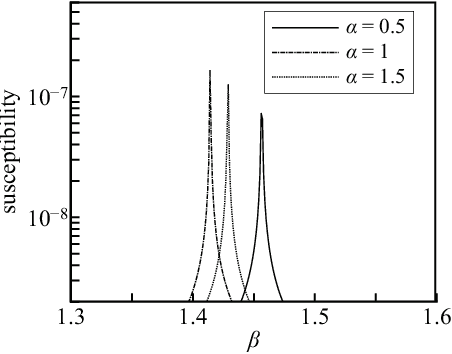
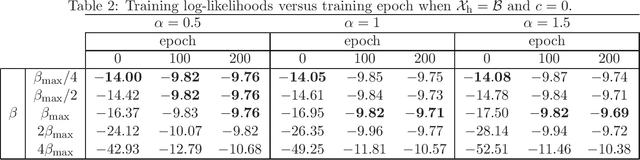
In feed-forward neural networks, dataset-free weight-initialization method such as LeCun, Xavier (or Glorot), and He initializations have been developed. These methods randomly determine the initial values of weight parameters based on specific distributions (e.g., Gaussian or uniform distributions) without using training datasets. To the best of the authors' knowledge, such a dataset-free weight-initialization method is yet to be developed for restricted Boltzmann machines (RBMs), which are probabilistic neural networks consisting of two layers, In this study, we derive a dataset-free weight-initialization method for Bernoulli--Bernoulli RBMs based on a statistical mechanical analysis. In the proposed weight-initialization method, the weight parameters are drawn from a Gaussian distribution with zero mean. The standard deviation of the Gaussian distribution is optimized based on our hypothesis which is that a standard deviation providing a larger layer correlation (LC) between the two layers improves the learning efficiency. The expression of the LC is derived based on a statistical mechanical analysis. The optimal value of the standard deviation corresponds to the maximum point of the LC. The proposed weight-initialization method is identical to Xavier initialization in a specific case (i.e., in the case the sizes of the two layers are the same, the random variables of the layers are $\{-1,1\}$-binary, and all bias parameters are zero).

Free Energy Evaluation Using Marginalized Annealed Importance Sampling

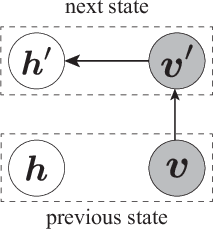
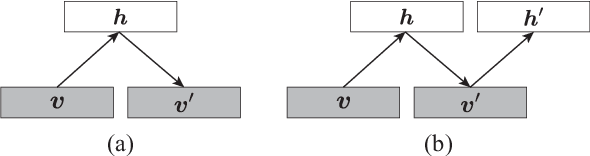
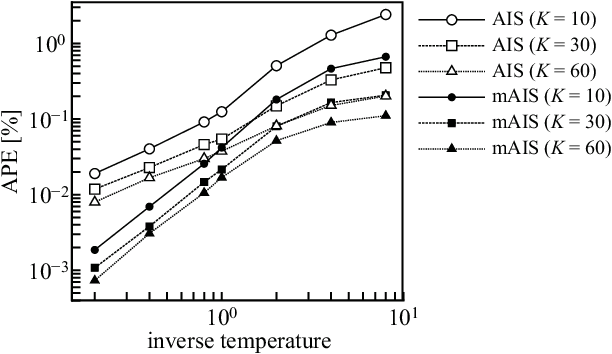
The evaluation of the free energy of a stochastic model is considered to be a significant issue in various fields of physics and machine learning. However, the exact free energy evaluation is computationally infeasible because it includes an intractable partition function. Annealed importance sampling (AIS) is a type of importance sampling based on the Markov chain Monte Carlo method, which is similar to a simulated annealing, and can effectively approximate the free energy. This study proposes a new AIS-based approach, referred to as marginalized AIS (mAIS). The statistical efficiency of mAIS is investigated in detail based on a theoretical and numerical perspectives. Based on the investigation, it has been proved that mAIS is more effective than AIS under a certain condition.

Mean-Field Inference in Gaussian Restricted Boltzmann Machine

A Gaussian restricted Boltzmann machine (GRBM) is a Boltzmann machine defined on a bipartite graph and is an extension of usual restricted Boltzmann machines. A GRBM consists of two different layers: a visible layer composed of continuous visible variables and a hidden layer composed of discrete hidden variables. In this paper, we derive two different inference algorithms for GRBMs based on the naive mean-field approximation (NMFA). One is an inference algorithm for whole variables in a GRBM, and the other is an inference algorithm for partial variables in a GBRBM. We compare the two methods analytically and numerically and show that the latter method is better.