Ryosuke Maeno
Dataset-Free Weight-Initialization on Restricted Boltzmann Machine
Sep 12, 2024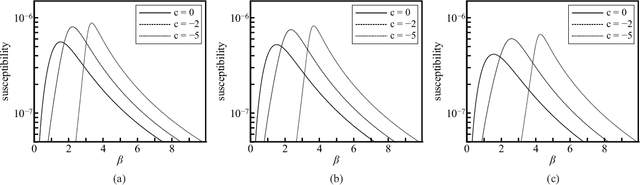
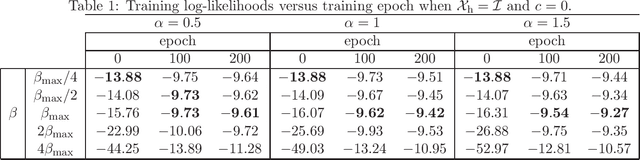
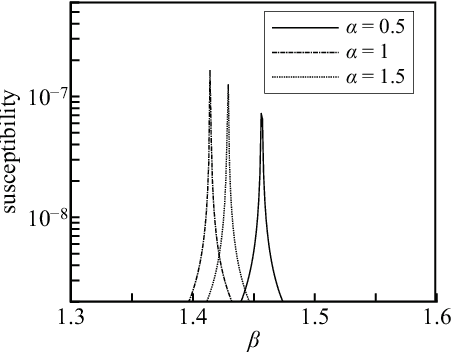
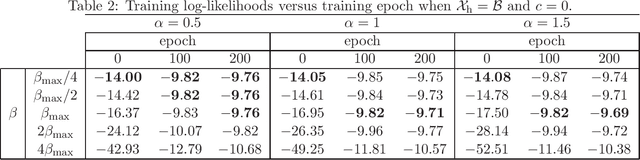
Abstract:In feed-forward neural networks, dataset-free weight-initialization method such as LeCun, Xavier (or Glorot), and He initializations have been developed. These methods randomly determine the initial values of weight parameters based on specific distributions (e.g., Gaussian or uniform distributions) without using training datasets. To the best of the authors' knowledge, such a dataset-free weight-initialization method is yet to be developed for restricted Boltzmann machines (RBMs), which are probabilistic neural networks consisting of two layers, In this study, we derive a dataset-free weight-initialization method for Bernoulli--Bernoulli RBMs based on a statistical mechanical analysis. In the proposed weight-initialization method, the weight parameters are drawn from a Gaussian distribution with zero mean. The standard deviation of the Gaussian distribution is optimized based on our hypothesis which is that a standard deviation providing a larger layer correlation (LC) between the two layers improves the learning efficiency. The expression of the LC is derived based on a statistical mechanical analysis. The optimal value of the standard deviation corresponds to the maximum point of the LC. The proposed weight-initialization method is identical to Xavier initialization in a specific case (i.e., in the case the sizes of the two layers are the same, the random variables of the layers are $\{-1,1\}$-binary, and all bias parameters are zero).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge