Free Energy Evaluation Using Marginalized Annealed Importance Sampling

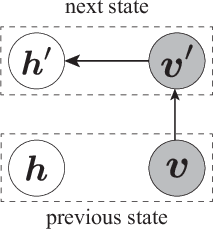
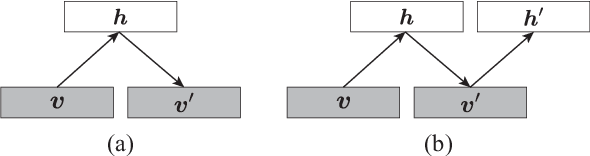
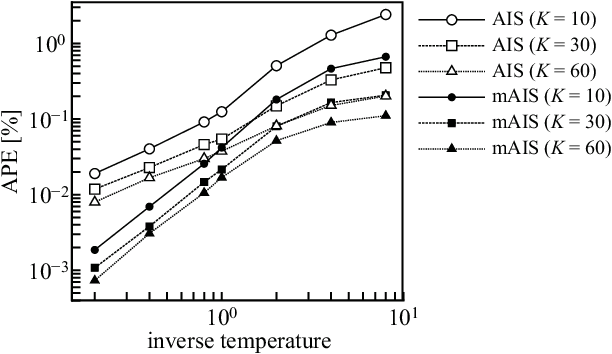
The evaluation of the free energy of a stochastic model is considered to be a significant issue in various fields of physics and machine learning. However, the exact free energy evaluation is computationally infeasible because it includes an intractable partition function. Annealed importance sampling (AIS) is a type of importance sampling based on the Markov chain Monte Carlo method, which is similar to a simulated annealing, and can effectively approximate the free energy. This study proposes a new AIS-based approach, referred to as marginalized AIS (mAIS). The statistical efficiency of mAIS is investigated in detail based on a theoretical and numerical perspectives. Based on the investigation, it has been proved that mAIS is more effective than AIS under a certain condition.