Actively Inferring Optimal Measurement Sequences

Measurement of a physical quantity such as light intensity is an integral part of many reconstruction and decision scenarios but can be costly in terms of acquisition time, invasion of or damage to the environment and storage. Data minimisation and compliance with data protection laws is also an important consideration. Where there are a range of measurements that can be made, some may be more informative and compliant with the overall measurement objective than others. We develop an active sequential inference algorithm that uses the low dimensional representational latent space from a variational autoencoder (VAE) to choose which measurement to make next. Our aim is to recover high dimensional data by making as few measurements as possible. We adapt the VAE encoder to map partial data measurements on to the latent space of the complete data. The algorithm draws samples from this latent space and uses the VAE decoder to generate data conditional on the partial measurements. Estimated measurements are made on the generated data and fed back through the partial VAE encoder to the latent space where they can be evaluated prior to making a measurement. Starting from no measurements and a normal prior on the latent space, we consider alternative strategies for choosing the next measurement and updating the predictive posterior prior for the next step. The algorithm is illustrated using the Fashion MNIST dataset and a novel convolutional Hadamard pattern measurement basis. We see that useful patterns are chosen within 10 steps, leading to the convergence of the guiding generative images. Compared with using stochastic variational inference to infer the parameters of the posterior distribution for each generated data point individually, the partial VAE framework can efficiently process batches of generated data and obtains superior results with minimal measurements.

Deceptive Diffusion: Generating Synthetic Adversarial Examples

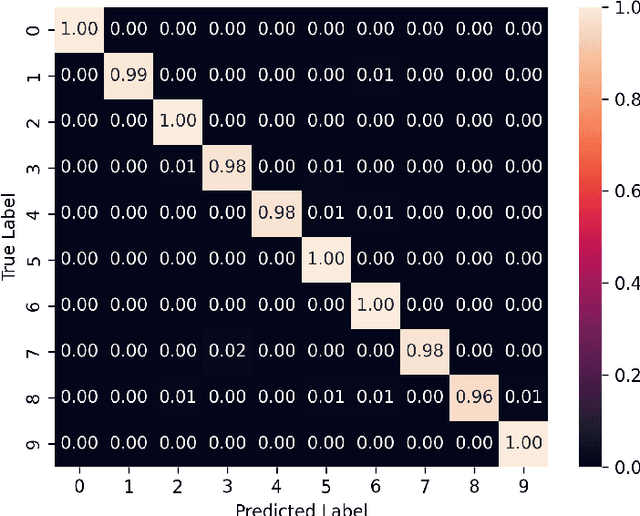
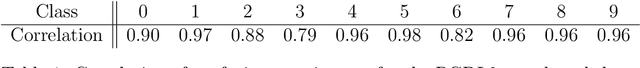
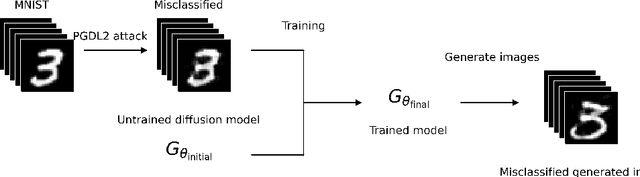
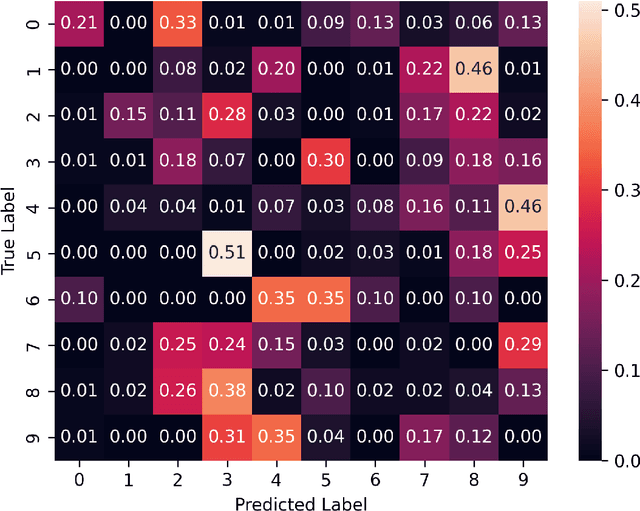
We introduce the concept of deceptive diffusion -- training a generative AI model to produce adversarial images. Whereas a traditional adversarial attack algorithm aims to perturb an existing image to induce a misclassificaton, the deceptive diffusion model can create an arbitrary number of new, misclassified images that are not directly associated with training or test images. Deceptive diffusion offers the possibility of strengthening defence algorithms by providing adversarial training data at scale, including types of misclassification that are otherwise difficult to find. In our experiments, we also investigate the effect of training on a partially attacked data set. This highlights a new type of vulnerability for generative diffusion models: if an attacker is able to stealthily poison a portion of the training data, then the resulting diffusion model will generate a similar proportion of misleading outputs.

Diffusion Models for Generative Artificial Intelligence: An Introduction for Applied Mathematicians

Generative artificial intelligence (AI) refers to algorithms that create synthetic but realistic output. Diffusion models currently offer state of the art performance in generative AI for images. They also form a key component in more general tools, including text-to-image generators and large language models. Diffusion models work by adding noise to the available training data and then learning how to reverse the process. The reverse operation may then be applied to new random data in order to produce new outputs. We provide a brief introduction to diffusion models for applied mathematicians and statisticians. Our key aims are (a) to present illustrative computational examples, (b) to give a careful derivation of the underlying mathematical formulas involved, and (c) to draw a connection with partial differential equation (PDE) diffusion models. We provide code for the computational experiments. We hope that this topic will be of interest to advanced undergraduate students and postgraduate students. Portions of the material may also provide useful motivational examples for those who teach courses in stochastic processes, inference, machine learning, PDEs or scientific computing.

Quantum Deep Learning: Sampling Neural Nets with a Quantum Annealer

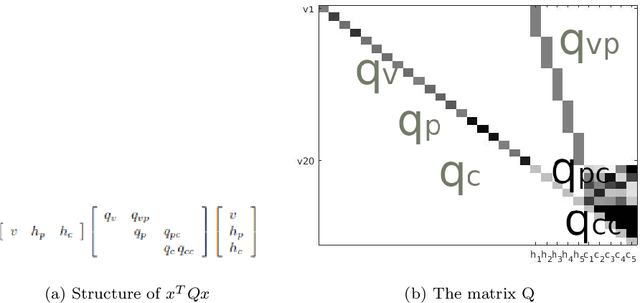
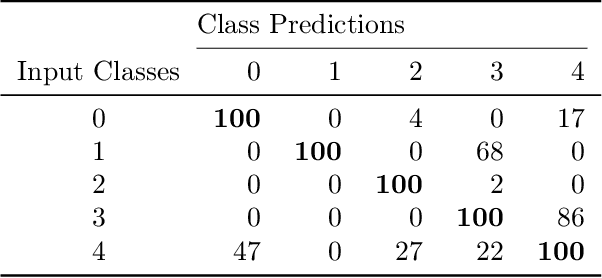
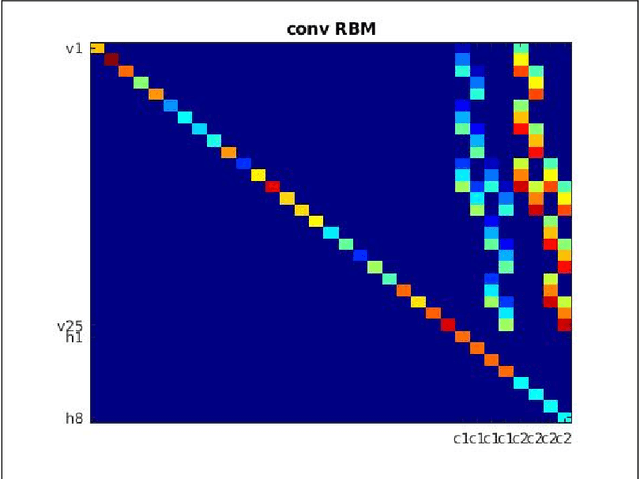
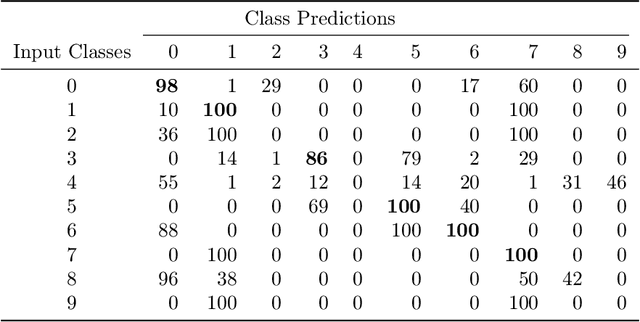
We demonstrate the feasibility of framing a classically learned deep neural network as an energy based model that can be processed on a one-step quantum annealer in order to exploit fast sampling times. We propose approaches to overcome two hurdles for high resolution image classification on a quantum processing unit (QPU): the required number and binary nature of the model states. With this novel method we successfully transfer a convolutional neural network to the QPU and show the potential for classification speedup of at least one order of magnitude.

Deep Learning: An Introduction for Applied Mathematicians

Multilayered artificial neural networks are becoming a pervasive tool in a host of application fields. At the heart of this deep learning revolution are familiar concepts from applied and computational mathematics; notably, in calculus, approximation theory, optimization and linear algebra. This article provides a very brief introduction to the basic ideas that underlie deep learning from an applied mathematics perspective. Our target audience includes postgraduate and final year undergraduate students in mathematics who are keen to learn about the area. The article may also be useful for instructors in mathematics who wish to enliven their classes with references to the application of deep learning techniques. We focus on three fundamental questions: what is a deep neural network? how is a network trained? what is the stochastic gradient method? We illustrate the ideas with a short MATLAB code that sets up and trains a network. We also show the use of state-of-the art software on a large scale image classification problem. We finish with references to the current literature.