Multi-View Photometric Stereo Revisited

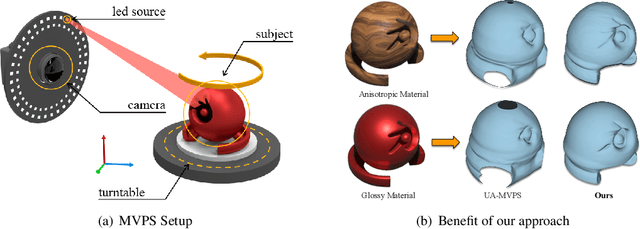
Multi-view photometric stereo (MVPS) is a preferred method for detailed and precise 3D acquisition of an object from images. Although popular methods for MVPS can provide outstanding results, they are often complex to execute and limited to isotropic material objects. To address such limitations, we present a simple, practical approach to MVPS, which works well for isotropic as well as other object material types such as anisotropic and glossy. The proposed approach in this paper exploits the benefit of uncertainty modeling in a deep neural network for a reliable fusion of photometric stereo (PS) and multi-view stereo (MVS) network predictions. Yet, contrary to the recently proposed state-of-the-art, we introduce neural volume rendering methodology for a trustworthy fusion of MVS and PS measurements. The advantage of introducing neural volume rendering is that it helps in the reliable modeling of objects with diverse material types, where existing MVS methods, PS methods, or both may fail. Furthermore, it allows us to work on neural 3D shape representation, which has recently shown outstanding results for many geometric processing tasks. Our suggested new loss function aims to fits the zero level set of the implicit neural function using the most certain MVS and PS network predictions coupled with weighted neural volume rendering cost. The proposed approach shows state-of-the-art results when tested extensively on several benchmark datasets.

Uncertainty-Aware Deep Multi-View Photometric Stereo

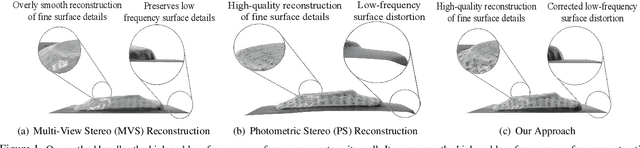
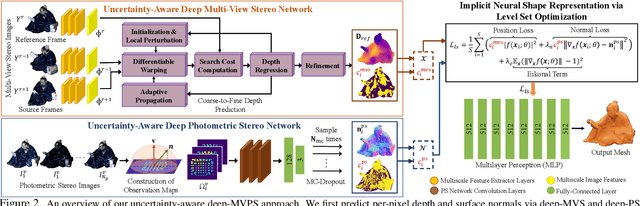
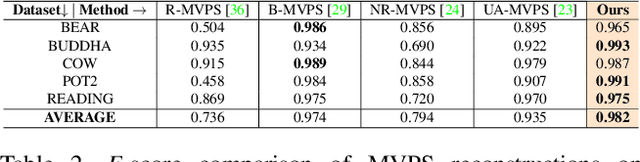
This paper presents a simple and effective solution to the longstanding classical multi-view photometric stereo (MVPS) problem. It is well-known that photometric stereo (PS) is excellent at recovering high-frequency surface details, whereas multi-view stereo (MVS) can help remove the low-frequency distortion due to PS and retain the global geometry of the shape. This paper proposes an approach that can effectively utilize such complementary strengths of PS and MVS. Our key idea is to combine them suitably while considering the per-pixel uncertainty of their estimates. To this end, we estimate per-pixel surface normals and depth using an uncertainty-aware deep-PS network and deep-MVS network, respectively. Uncertainty modeling helps select reliable surface normal and depth estimates at each pixel which then act as a true representative of the dense surface geometry. At each pixel, our approach either selects or discards deep-PS and deep-MVS network prediction depending on the prediction uncertainty measure. For dense, detailed, and precise inference of the object's surface profile, we propose to learn the implicit neural shape representation via a multilayer perceptron (MLP). Our approach encourages the MLP to converge to a natural zero-level set surface using the confident prediction from deep-PS and deep-MVS networks, providing superior dense surface reconstruction. Extensive experiments on the DiLiGenT-MV benchmark dataset show that our method provides high-quality shape recovery with a much lower memory footprint while outperforming almost all of the existing approaches.

Uncalibrated Neural Inverse Rendering for Photometric Stereo of General Surfaces

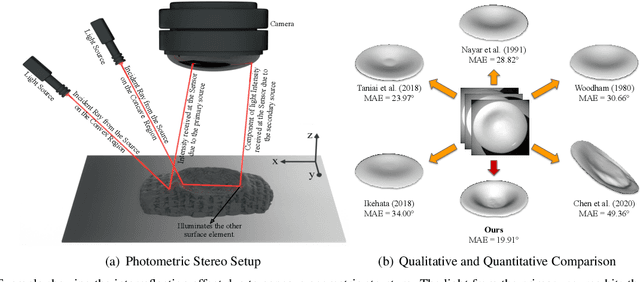
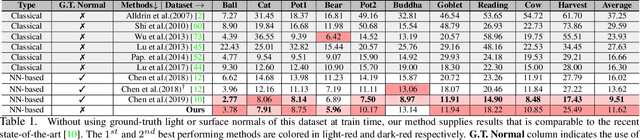
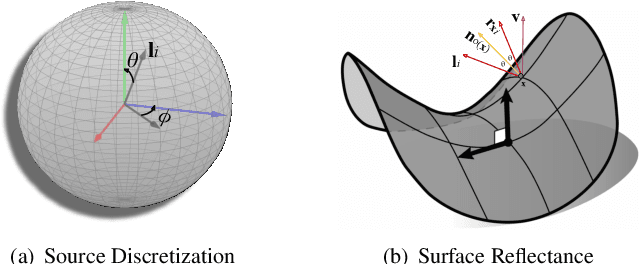
This paper presents an uncalibrated deep neural network framework for the photometric stereo problem. For training models to solve the problem, existing neural network-based methods either require exact light directions or ground-truth surface normals of the object or both. However, in practice, it is challenging to procure both of this information precisely, which restricts the broader adoption of photometric stereo algorithms for vision application. To bypass this difficulty, we propose an uncalibrated neural inverse rendering approach to this problem. Our method first estimates the light directions from the input images and then optimizes an image reconstruction loss to calculate the surface normals, bidirectional reflectance distribution function value, and depth. Additionally, our formulation explicitly models the concave and convex parts of a complex surface to consider the effects of interreflections in the image formation process. Extensive evaluation of the proposed method on the challenging subjects generally shows comparable or better results than the supervised and classical approaches.