Phase retrieval: Global convergence of gradient descent with optimal sample complexity

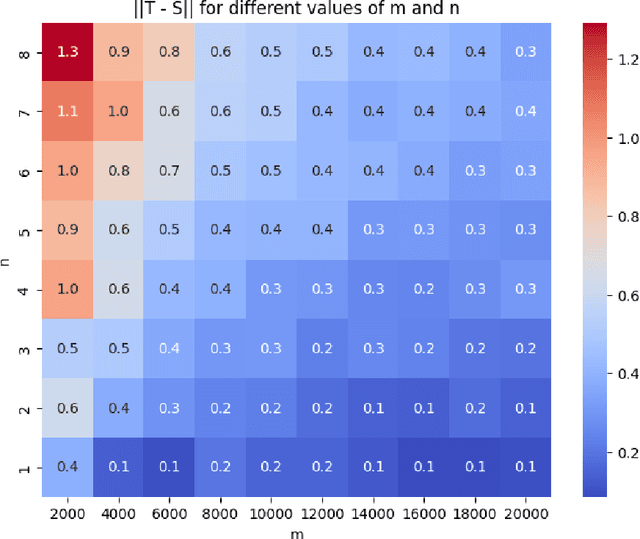
This paper addresses the phase retrieval problem, which aims to recover a signal vector $x$ from $m$ measurements $y_i=|\langle a_i,x^{\natural}\rangle|^2$, $i=1,\ldots,m$. A standard approach is to solve a nonconvex least squares problem using gradient descent with random initialization, which is known to work efficiently given a sufficient number of measurements. However, whether $O(n)$ measurements suffice for gradient descent to recover the ground truth efficiently has remained an open question. Prior work has established that $O(n\,{\rm poly}(\log n))$ measurements are sufficient. In this paper, we resolve this open problem by proving that $m=O(n)$ Gaussian random measurements are sufficient to guarantee, with high probability, that the objective function has a benign global landscape. This sample complexity is optimal because at least $\Omega(n)$ measurements are required for exact recovery. The landscape result allows us to further show that gradient descent with a constant step size converges to the ground truth from almost any initial point.

How Much Restricted Isometry is Needed In Nonconvex Matrix Recovery?

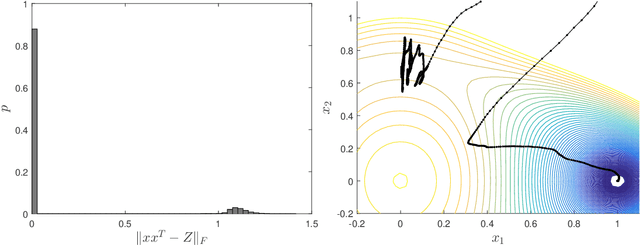
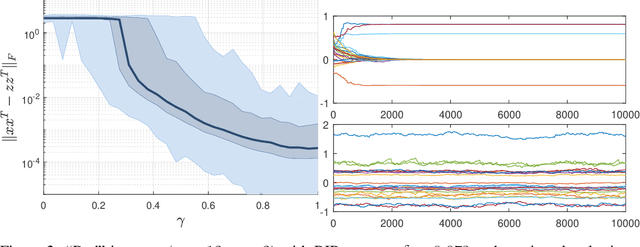
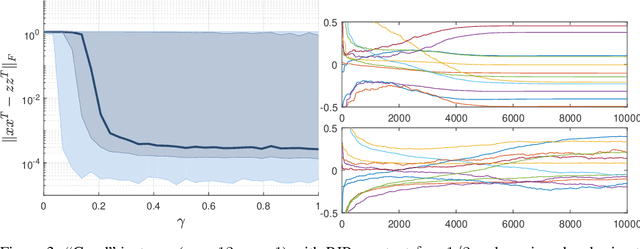
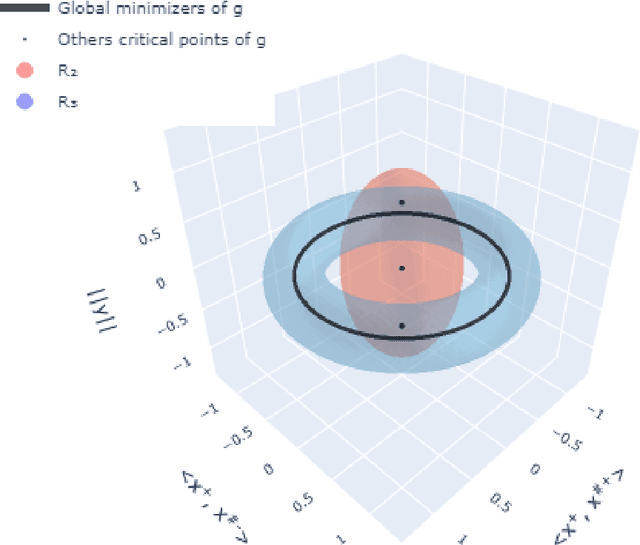
When the linear measurements of an instance of low-rank matrix recovery satisfy a restricted isometry property (RIP)---i.e. they are approximately norm-preserving---the problem is known to contain no spurious local minima, so exact recovery is guaranteed. In this paper, we show that moderate RIP is not enough to eliminate spurious local minima, so existing results can only hold for near-perfect RIP. In fact, counterexamples are ubiquitous: we prove that every x is the spurious local minimum of a rank-1 instance of matrix recovery that satisfies RIP. One specific counterexample has RIP constant $\delta=1/2$, but causes randomly initialized stochastic gradient descent (SGD) to fail 12% of the time. SGD is frequently able to avoid and escape spurious local minima, but this empirical result shows that it can occasionally be defeated by their existence. Hence, while exact recovery guarantees will likely require a proof of no spurious local minima, arguments based solely on norm preservation will only be applicable to a narrow set of nearly-isotropic instances.