FT K-Means: A High-Performance K-Means on GPU with Fault Tolerance

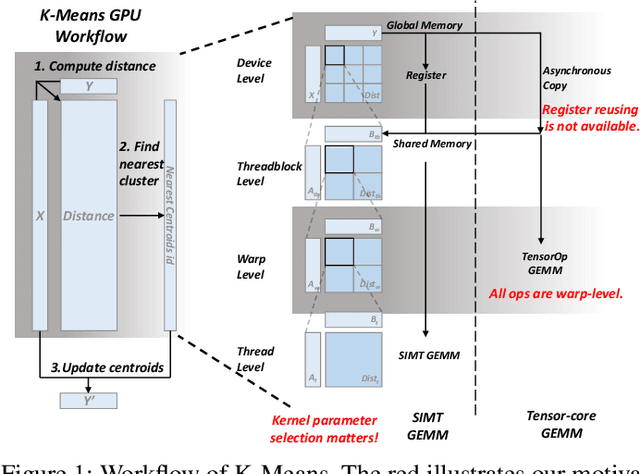
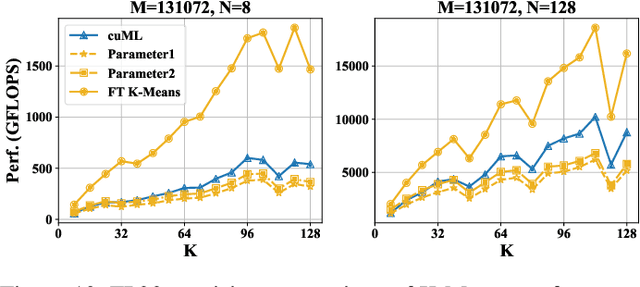
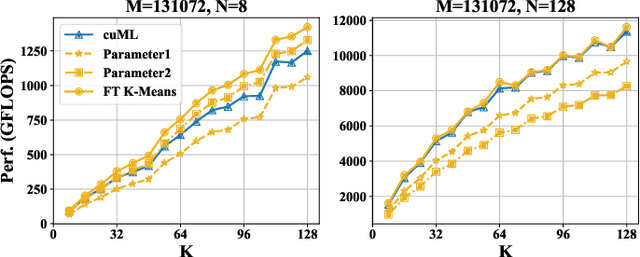
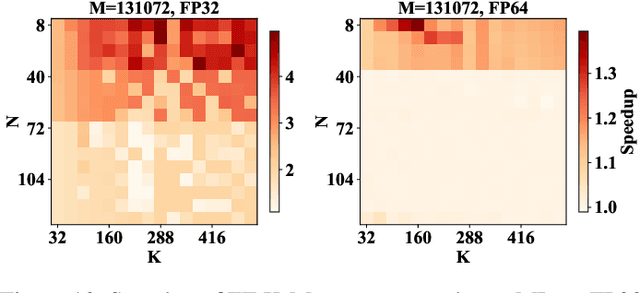
K-Means is a widely used algorithm in clustering, however, its efficiency is primarily constrained by the computational cost of distance computing. Existing implementations suffer from suboptimal utilization of computational units and lack resilience against soft errors. To address these challenges, we introduce FT K-Means, a high-performance GPU-accelerated implementation of K-Means with online fault tolerance. We first present a stepwise optimization strategy that achieves competitive performance compared to NVIDIA's cuML library. We further improve FT K-Means with a template-based code generation framework that supports different data types and adapts to different input shapes. A novel warp-level tensor-core error correction scheme is proposed to address the failure of existing fault tolerance methods due to memory asynchronization during copy operations. Our experimental evaluations on NVIDIA T4 GPU and A100 GPU demonstrate that FT K-Means without fault tolerance outperforms cuML's K-Means implementation, showing a performance increase of 10\%-300\% in scenarios involving irregular data shapes. Moreover, the fault tolerance feature of FT K-Means introduces only an overhead of 11\%, maintaining robust performance even with tens of errors injected per second.

Cost-Effective Methodology for Complex Tuning Searches in HPC: Navigating Interdependencies and Dimensionality

Tuning searches are pivotal in High-Performance Computing (HPC), addressing complex optimization challenges in computational applications. The complexity arises not only from finely tuning parameters within routines but also potential interdependencies among them, rendering traditional optimization methods inefficient. Instead of scrutinizing interdependencies among parameters and routines, practitioners often face the dilemma of conducting independent tuning searches for each routine, thereby overlooking interdependence, or pursuing a more resource-intensive joint search for all routines. This decision is driven by the consideration that some interdependence analysis and high-dimensional decomposition techniques in literature may be prohibitively expensive in HPC tuning searches. Our methodology adapts and refines these methods to ensure computational feasibility while maximizing performance gains in real-world scenarios. Our methodology leverages a cost-effective interdependence analysis to decide whether to merge several tuning searches into a joint search or conduct orthogonal searches. Tested on synthetic functions with varying levels of parameter interdependence, our methodology efficiently explores the search space. In comparison to Bayesian-optimization-based full independent or fully joint searches, our methodology suggested an optimized breakdown of independent and merged searches that led to final configurations up to 8% more accurate, reducing the search time by up to 95%. When applied to GPU-offloaded Real-Time Time-Dependent Density Functional Theory (RT-TDDFT), an application in computational materials science that challenges modern HPC autotuners, our methodology achieved an effective tuning search. Its adaptability and efficiency extend beyond RT-TDDFT, making it valuable for related applications in HPC.