Breno W. S. R. de Carvalho
Neuro-Symbolic Inductive Logic Programming with Logical Neural Networks
Dec 06, 2021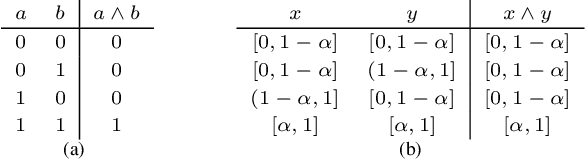

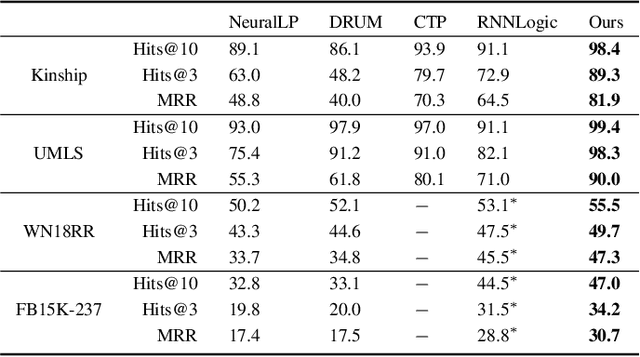
Abstract:Recent work on neuro-symbolic inductive logic programming has led to promising approaches that can learn explanatory rules from noisy, real-world data. While some proposals approximate logical operators with differentiable operators from fuzzy or real-valued logic that are parameter-free thus diminishing their capacity to fit the data, other approaches are only loosely based on logic making it difficult to interpret the learned "rules". In this paper, we propose learning rules with the recently proposed logical neural networks (LNN). Compared to others, LNNs offer strong connection to classical Boolean logic thus allowing for precise interpretation of learned rules while harboring parameters that can be trained with gradient-based optimization to effectively fit the data. We extend LNNs to induce rules in first-order logic. Our experiments on standard benchmarking tasks confirm that LNN rules are highly interpretable and can achieve comparable or higher accuracy due to their flexible parameterization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge