Distributed AI Platform for the 6G RAN

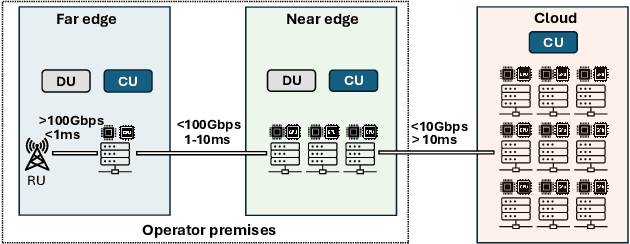
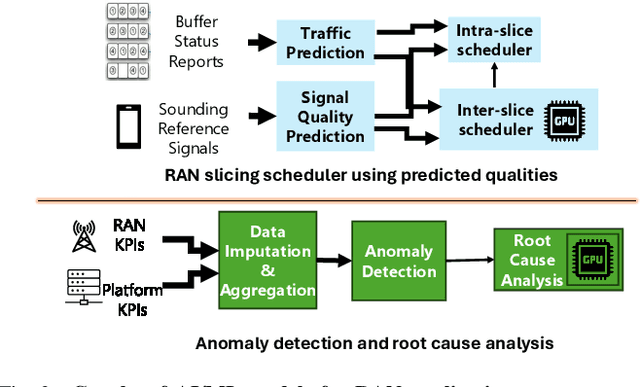
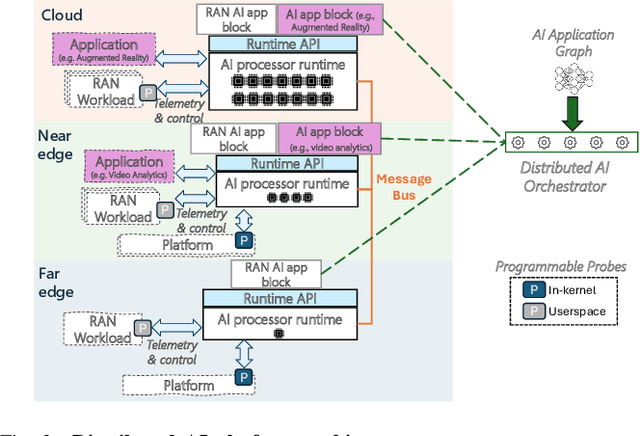
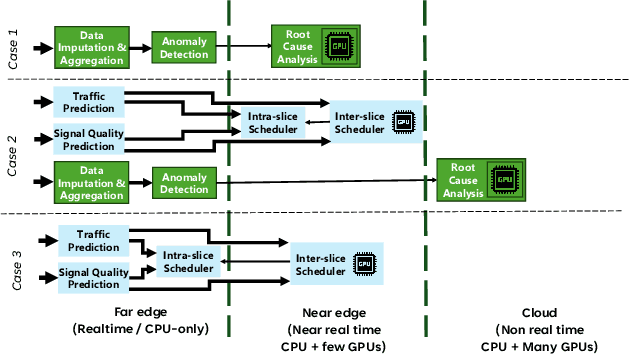
Cellular Radio Access Networks (RANs) are rapidly evolving towards 6G, driven by the need to reduce costs and introduce new revenue streams for operators and enterprises. In this context, AI emerges as a key enabler in solving complex RAN problems spanning both the management and application domains. Unfortunately, and despite the undeniable promise of AI, several practical challenges still remain, hindering the widespread adoption of AI applications in the RAN space. This article attempts to shed light to these challenges and argues that existing approaches in addressing them are inadequate for realizing the vision of a truly AI-native 6G network. Motivated by this lack of solutions, it proposes a generic distributed AI platform architecture, tailored to the needs of an AI-native RAN and discusses its alignment with ongoing standardization efforts.

Distributed Non-Stochastic Experts

We consider the online distributed non-stochastic experts problem, where the distributed system consists of one coordinator node that is connected to $k$ sites, and the sites are required to communicate with each other via the coordinator. At each time-step $t$, one of the $k$ site nodes has to pick an expert from the set ${1, ..., n}$, and the same site receives information about payoffs of all experts for that round. The goal of the distributed system is to minimize regret at time horizon $T$, while simultaneously keeping communication to a minimum. The two extreme solutions to this problem are: (i) Full communication: This essentially simulates the non-distributed setting to obtain the optimal $O(\sqrt{\log(n)T})$ regret bound at the cost of $T$ communication. (ii) No communication: Each site runs an independent copy : the regret is $O(\sqrt{log(n)kT})$ and the communication is 0. This paper shows the difficulty of simultaneously achieving regret asymptotically better than $\sqrt{kT}$ and communication better than $T$. We give a novel algorithm that for an oblivious adversary achieves a non-trivial trade-off: regret $O(\sqrt{k^{5(1+\epsilon)/6} T})$ and communication $O(T/k^{\epsilon})$, for any value of $\epsilon \in (0, 1/5)$. We also consider a variant of the model, where the coordinator picks the expert. In this model, we show that the label-efficient forecaster of Cesa-Bianchi et al. (2005) already gives us strategy that is near optimal in regret vs communication trade-off.