A KL-based Analysis Framework with Applications to Non-Descent Optimization Methods

We propose a novel analysis framework for non-descent-type optimization methodologies in nonconvex scenarios based on the Kurdyka-Lojasiewicz property. Our framework allows covering a broad class of algorithms, including those commonly employed in stochastic and distributed optimization. Specifically, it enables the analysis of first-order methods that lack a sufficient descent property and do not require access to full (deterministic) gradient information. We leverage this framework to establish, for the first time, iterate convergence and the corresponding rates for the decentralized gradient method and federated averaging under mild assumptions. Furthermore, based on the new analysis techniques, we show the convergence of the random reshuffling and stochastic gradient descent method without necessitating typical a priori bounded iterates assumptions.

Convergence of SGD with momentum in the nonconvex case: A novel time window-based analysis

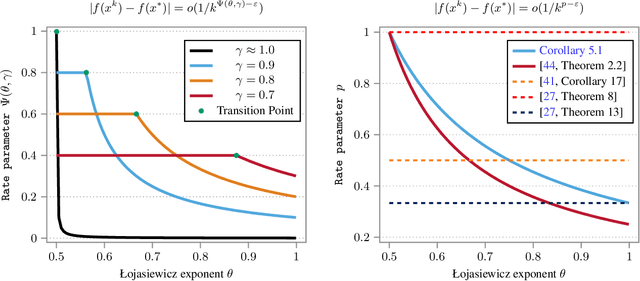
We propose a novel time window-based analysis technique to investigate the convergence behavior of the stochastic gradient descent method with momentum (SGDM) in nonconvex settings. Despite its popularity, the convergence behavior of SGDM remains less understood in nonconvex scenarios. This is primarily due to the absence of a sufficient descent property and challenges in controlling stochastic errors in an almost sure sense. To address these challenges, we study the behavior of SGDM over specific time windows, rather than examining the descent of consecutive iterates as in traditional analyses. This time window-based approach simplifies the convergence analysis and enables us to establish the first iterate convergence result for SGDM under the Kurdyka-Lojasiewicz (KL) property. Based on the underlying KL exponent and the utilized step size scheme, we further characterize local convergence rates of SGDM.